Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 5.Problemas Propostos - Ex. 59
O plano intercepta os eixos cartesianos nos pontos e . Calcular a área do triângulo .
Passo 1
Nós temos um plano e dentro desse plano temos pontos que interceptam os eixos cartesianos, e formam um triângulo:
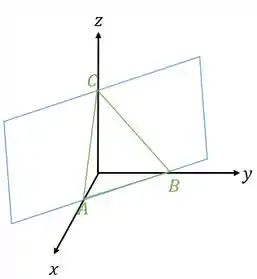
Vamos começar com o ponto que toca o eixo , isso significa que já que o ponto não toca esses eixos e aplicando na função do plano, teremos:
O ponto pode ser dado por .
Passo 2
Agora, podemos calcular o ponto que toca o eixo , onde :
O ponto pode ser dado por
E por fim, calcularemos o ponto que toca o eixo , onde :
O ponto pode ser dado por .
Passo 3
Sabemos que o produto entre dois vetores nos fornece a área de um paralelogramo, e que um triângulo é a metade do paralelogramo:
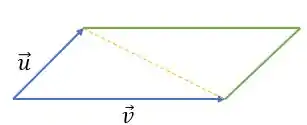
Então, precisamos encontrar dois vetores para fazer o produto vetorial, encontrar o módulo desse produto vetorial e dividir por dois. Bora lá?
Uma forma de encontrar dois vetores desse problema é usar os segmentos de reta, ou seja, a distância em que cada ponto tem do outro. Pensa assim, temos um triângulo e com isso temos três pontos, qual a distância entre eles?
Vamos pegar a distância entre e ,e a distância entre e , e chamaremos de vetores e , e pode ser dado por:
Com esses dois vetores, podemos montar o produto vetorial entre eles:
Colocamos a resposta como que significa unidades de área.