Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 2.Problemas - Ex. 8
Com argumento análogo ao do exercício, anterior, determine o simétrico do ponto em relação à diagonal
Passo 1
Falaaaa,blz??? Para essa questão vamos tentar usar a ideia da questão anterior, formar um quadrado e determinar o vértice oposto ao A, tendo que uma de suas diagonais pertence à
Passo 2
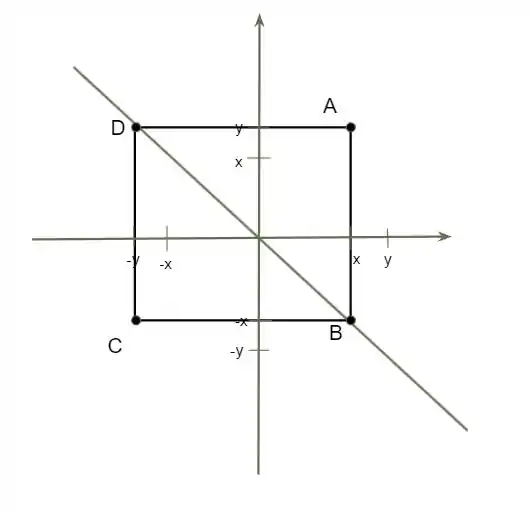
Para criar o desenho, primeiro faça os eixos, marque um ponto A e depois outros 2 pontos sobre a reta , esses 2 pontos ligados serão 1 das diagonais. Lembrando que a escolha desses 2 pontos deve ser tal que após ligados com A, sejam paralelos aos eixos. Depois fica direto achar o outro ponto, seria algo mais ou menos assim:
Passo 3
Ou seja, o vértice oposto ao A no quadrado é o C = (-y,-x).
Resposta
Exercícios de Livros Relacionados
Quais dos seguintes pares de planos se cortam segundo uma reta? x + 2 y - 3 z - 4 = 0 ex - 4 y + 2 z + 1 = 0 2 x - y + 4 z + 3 = 0e4 x - 2 y + 8 z = 0 x - y = 0ex + z = 0
Considere as retas x , y , z = t ( 1,2 , - 3 ) e x , y , z = 0,1 , 2 + s ( 2,4 , - 6 ). Encontre a equação geral do plano que contém estas duas retas.
Seja a x + b y + c z + d = 0 a equação de um plano π com a b c d ≠ 0 . (a) Determine a interseção de π com os eixos; (b) Se P 1 = ( p 1 , 0,0 ) , P 2 = ( 0 , p 2 , 0 ) e P 3 = 0,0 , p 3 são as interse
(a) Verifique que a reta r : (x, y, z) = (1, 0, 1) + t(1, −1, 0) e paralela ao plano π : x + y + z = 0. (b) Calcule a distância de r a π.(c) Existem retas contidas no plano π, que são reversas à reta
Obtenha uma equação geral do plano π, que contém a reta: r :x - 2 y + 2 z = 0 3 x - 5 y + 7 z = 0 e forma com o plano π 1 : x + z = 0 um angulo de 60 ° .