Enunciado
Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 4.1 - Ex. 1g
Faça um esboço dos seguintes planos: (g):
Passo 1
Oi, pessoal! Tudo bem? 😊
Para representarmos o plano precisamos de seu vetor ortogonal e um ponto que pertença a esse plano.
Passo 2
é dado na equação do plano, portanto:
Um ponto que pertence ao plano é:
Passo 3
Temos como esboço de
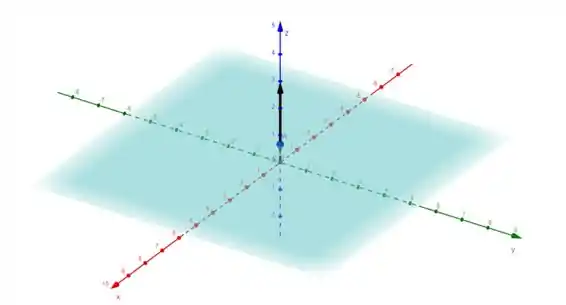
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Determine a equação do plano constituído de todos os pontos que são equidistantes dos pontos ( 2 , 5,5 ) e ( - 6,3 , 1 ) .
Determine as equações paramétricas da reta que passa pelo ponto ( 0 , 1,2 ) , é paralela ao plano x + y + z = 2 e perpendicular à reta x = 1 + t , y = 1 - t , z = 2 t .
Determine a equação do plano constituído de todos os pontos que são equidistantes dos pontos ( 1 , 0 , - 2 ) e ( 3,4 , 0 ) .
Determine as equações paramétricas da reta que passa pelo ponto ( 0 , 1,2 ) , é perpendicular à reta x = 1 + t , y = 1 - t , z = 2 t , e intercepta essa reta.
Quais das quatro retas seguintes são paralelos? Existem duas coincidentes? L 1 : x = 1 + t ,y = t ,z = 2 - 5 t L 2 : x + 1 = y - 2 = 1 - z L 3 :x = 1 + t ,y =4 + t ,z = 1 - t L 4 : r → = 2,1 , - 3 + t