Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 3.Problemas propostos - Ex. 29

29. Os pontos médios dos lados do triângulo A B C são M 0,1 , 3 , N 3 , - 2,2 e P 1,0 , 2 . Determinar a área do triângulo A B C .

Passo 1

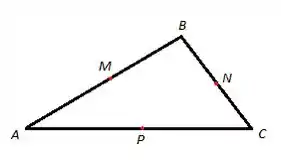
Para calcular a área do triângulo A B C :

A A B C = 1 2 A B → × A C →

E como M ,   N   e P   são pontos médios, então temos:

M = A + B 2

N = B + C 2

P = A + C 2

Passo 2

Vamos achar esses vetores:

A B → = B - A

Repare que se fizermos:

N - P = B + C 2 - A + C 2

N - P = B - A 2

B - A = 2 N - P

Então:

A B → = 2 N - P

A B → = 2 3 , - 2,2 - 1,0 , 2

A B → = 2 2 , - 2,0

A B → = 4 , - 4,0

E o outro vetor:

A C → = C - A

Repare que se fizermos:

N - M = B + C 2 - A + B 2

N - M = C - A 2

C - A = 2 N - M

Então:

A C → = 2 N - M

A C → = 2 3 , - 2,2 - 0,1 , 3

A C → = 2 3 , - 3 , - 1

A C → = 6 , - 6 , - 2

Passo 3

Fazendo o produto vetorial:

A B → × A C → = i ^ j ^ k ^ 4 - 4 0 6 - 6 - 2

A B → × A C → = - 4 - 2 i ^ + 0 6 j ^ + 4 - 6 k ^ - 6 - 4 k ^ - - 6 0 i ^ - - 2 4 j ^

A B → × A C → = 8 i ^ + 8 j ^

E calculando seu módulo:

A B → × A C → = 8 2 + 8 2

A B → × A C → = 8 2

Então, finalmente, a área do triângulo vai ser:

A A B C = 1 2 8 2

A A B C = 4 2

Resposta

A A B C = 4 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escrever enunciado aqui
Determine a . b para a =s , 2 s , 3 s e b =t , - t , 5 t
Determine o produto vetorial a × b e verifique que ele é ortogonal a a e b .
Determine o produto vetorial a × b e verifique que ele é ortogonal a a e b .
Encontre o vetor, não com determinantes, mas usando propriedades do produto vetorial. i + j × i - j