Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 5.Problemas Propostos - Ex. 50
Nos problemas 49 e 51, determinar o ponto de interseção da reta com o plano nos seguintes casos:
Passo 1
Queremos encontrar a inteseção da reta com o plano. Uma informação muito relevante dada pelo exercício é que o plano vai passar em um ponto onde no eixo cartesiano:
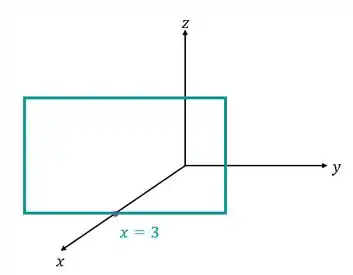
Isso significa que vamos resolver o sistema de equações onde .
Passo 2
Sendo o nosso sistema:
Começando com a equação , então:
Agora substituindo em :
E já está determinado que , isso significa que nosso ponto de interseção é dado por
Resposta
Exercícios de Livros Relacionados
Nos Problemas 19 a22 , os pares de retas r 1 e r 2 são paralelas ou concorrentes. Encontrar uma equação geral do plano que as contém.22) r 1 :x = z y = - 3 r 2 :x = - t y = 1 z = 2 - t
Nos Problemas 25 a 30 , obter uma equação geral do plano:28) Paralelo ao plano x O y e que contenha o ponto A ( 5 ,- 2 ,3 ) .
Nos Problemas 25 a 30 , obter uma equação geral do plano:27) Paralelo ao eixo y e que contenha os pontos A ( 2 ,3 ,0 ) e B ( 0 ,4 ,1 ) .
Nos Problemas 23 e 24 , determinar uma equação geral do plano que contenha o ponto e a reta dados:23) A 4,3 , 2 r :x = t y = 2 - t 3 + 2 t
Nos Problemas 25 a 30 , obter uma equação geral do plano:26) Paralelo ao eixo x e que contenha os pontos A ( - 2 ,0 ,2 ) e B ( 0 ,- 2 ,1 ) .