Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 25.Exercício - Ex. 41
Prove, em cada caso, que a equação dada descreve uma quádrica cônica.
(a)
(b)
(c)
(d)
(e)
Passo 1
Bom pessoal, o que significa provar que uma equação descreve uma quádrica cônica?
A forma mais fácil de conseguir isso, é mostrando que a equação pode ser descrita nessa forma aqui:
Em todos esses casos, só precisamos fazer algumas mudanças de coordenadas para deixar as equações nessa forma.
Passo 2
(a) Aqui o nosso problema é só uma confusão entre as variáveis , e .
A gente precisa que o esteja no lugar do , então vamos fazer uma rotação como essa aqui:
Então nesse caso o que aconteceu com os eixos foi:
Substituindo isso na equação:
Então:
Agora chegamos na forma geral do enunciado.
Passo 3
(b) Agora olhando para a segunda expressão:
Temos que trocar por , então vamos fazer o seguinte:
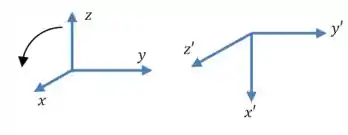
Ou seja, a transformação é:
Substituindo na equação:
Então:
Que é a forma reduzida que vimos lá em cima.
Passo 4
(c) Para a terceira equação:
Só precisamos fazer uma translação de coordenadas:
Que é só uma forma de “deslocar” a origem do nosso sistema de coordenadas, e nós podemos fazer isso livremente.
Substituindo na equação:
Que á a forma reduzida mais uma vez.
Passo 5
(d) Para a quarta equação:
Aqui primeiro vamos fazer uma translação igual a do passo anterior:
E agora fazemos uma rotação igual a do item (a):
Então:
Que é a forma reduzida!
Passo 6
(e) Por último, a equação é
Vamos fazer a translação de novo:
Para encontrar:
E agora vamos fazer a mesma rotação do item
Então:
Então essa também é uma quádrica cônica.
Resposta
Veja as demonstrações. Nos itens (a) e (b) usamos uma rotação dos eixos, e nos itens (c), (d) e (e) usamos rotações e translações.