Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 4.Exercícios Propostos - Ex. 22

A B C D é um quadrado, M e N são pontos médios dos lados, A B → =   a → e A D → =   b → . Determine em função de a → e b → :

  1. o vetor I C → ;
  2. a área do triângulo x = C I N .

Passo 1

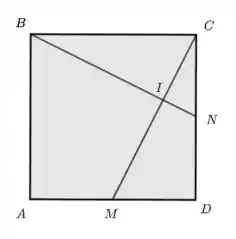
  1. Tudo beleza, gente? A primeira coisa que temos que notar nessa questão é que temos duas formas de obter o vetor I C → :

    2. I C → = α   M C → = α ( M B → + B C → ) = α ( 1 2 A B → + A D → ) = α ( 1 2 a → + b → )

    I C → = I N → + N C →

    Por outro lado, temos

    N C → = 1 2 B C → = 1 2 b →

    I N → = β D N → = β ( D C → + C N → ) = β ( D C → + 1 2 C B → ) = β ( A B → - 1 2 A D → ) = β ( a → - 1 2 b → )

    Agora, vamos substituir esses resultados na segunda expressão para I C → :

    I C → = I N → + N C → = β ( a → - 1 2 b → ) + 1 2 b → = β a → + 1 2 ( 1 - β ) b →

    Você se surpreenderia se eu dissesse que as duas expressões para I C → tem que ser iguais?Não, né? Mas isso nos dá o seguinte resultado

    α ( 1 2 a → + b → ) = β a → + 1 2 ( 1 - β ) b →

    ⇒ ( α 2 - β ) a → = 1 2 ( 1 - β - 2 α ) b →

    Como   a → e   b → são L.I., a equação acima só pode ser verdadeira se for nula em ambos os lados. Logo, devemos ter

    α 2 - β = 0 ⇒ β = α 2

    1 - β - 2 α = 0 ⇒ 1 - α 2 - 2 α = 0

    ⇒ 1 - 5 α 2 = 0 ⇒ α = 2 5

    ⇒ β = α 2 = 1 5

    Agora, substituímos α = 2 5 na primeira expressão para

    I C → = α ( 1 2 a → + b → ) = 2 5 ( 1 2 a → + b → ) = 1 5 a → + 2 5 b →

    Passo 2

  2. Para descobrimos a área desse triângulo, basta lembrar que a área do triângulo é dada por

A = 1 2 A l t u r a × l a r g u r a = 1 2 | I C → ∧   I N → |

Já calculamos o vetor I C → no item a). Para obter I N → , só precisamos substituir β = 1 5 em

I N → = β ( a → - 1 2 b → ) = 1 5 a → - 1 10 b →

Ok, então vamos calcular o produto vetorial e depois o módulo do resultado:

I C → ∧   I N → = ( 1 5 a → + 2 5 b → ) ∧ ( 1 5 a → - 1 10 b → ) = 1 25 a → ∧ a → + 2 25 b → ∧ a → - 1 50 a → ∧ b → - 2 50 b → ∧ b →

I C → ∧   I N → = 2 25 b → ∧ a → - 1 50 a → ∧ b → = - 1 50 a → ∧ b → - 2 25 a → ∧ b → = - 5 50 a → ∧ b → = - 1 10 a → ∧ b →

| I C → ∧   I N → | = 1 10 | a → ∧ b → | = 1 10 | a → | | b → | s e n   θ

onde θ é o ângulo entre os vetores. Como temos um quadrado, então θ = 90 º e | a → | = | b → | . Assim,

| I C → ∧   I N → | = 1 10 | a → ∧ b → | = 1 10 | a → | 2

⇒ A = 1 2 1 10 | a → | 2 = 1 20 | a → | 2

Resposta

  1. I C → = 1 5 a → + 2 5 b →
  2. A = 1 20 | a → | 2

Exercícios de Livros Relacionados

Efetuar:vec i xx vec k
Se vec u = 3 vec i - vec j - 2 vec k , vec v = 2 vec i + 4 vec j - vec k e vec w = - vec i + vec k , determinar:vec u xx vec v + vec u xx vec w
Se vec u = 3 vec i - vec j - 2 vec k , vec v = 2 vec i + 4 vec j - vec k e vec w = - vec i + vec k , determinar:vec u xx ( vec v xx vec w )
Determine a * b onde a =1,5 ; 0,4 e b =- 4,6
Ache o ângulo entre os seguintes pares de vetores: (a): 2 i → + j →ej → - k → ;