Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 4.Exercícios Propostos - Ex. 25

Construa uma base ortonormal positiva ( u → ,   v → ,   w → ) tal que u → seja paralelo a ( 1,2 , 2 ) e v → paralelo a ( 2,0 , - 1 ) .

Passo 1

Tudo bem, gente? Como u → é paralelo a ( 1,2 , 2 ) e v → é paralelo a ( 2,0 , - 1 ) , então devemos ter

u → = α ( 1,2 , 2 )

v → = β ( 2,0 , - 1 )

w → = ( a , b , c )

Passo 2

Agora, vamos calcular os produtos vetoriais de cada par de vetores:

  • Do primeiro vetor com o segundo:

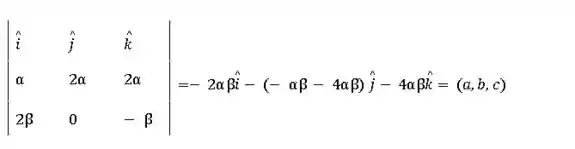
Então,

a = - 2 α β

b = 5 α β

c = - 4 α β

⇒   b = - 5 2 a ,   c = 2 a

  • Do segundo vetor com o terceiro:

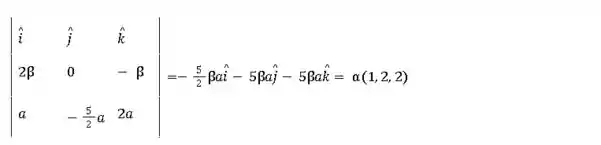
A única informação que obtemos desse produto vetorial é que

5 a β = - 2 α

  • Do terceiro vetor com o primeiro:

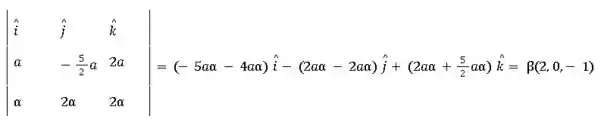
Agora, temos a seguinte informação:

- 9 a α = 2 β ⇒ β = - 9 2 a α

Passo 3

Substituímos o último resultado em:

5 a β = - 2 α ⇒ 5 a ( - 9 2 a α ) = - 2 α ⇒ 45 4 a 2 = 1 ⇒ a = 2 45 = 2 3 5 = 2 5 15

⇒   b = - 5 2 a = - 5 5 15 ,   c = 2 a = 4 5 15

w → = ( a , b , c ) = 5 15 ( 2 , - 5,4 )

Agora só falta determinar α , β . Para isso, temos duas equações:

β = - 9 2 a α = - 3 5 5 α

5 a β = - 2 α ⇒ 2 5 3 β = - 2 α ⇒ β = - 3 5 5 α

que geram o mesmo resultado. Mas calma que ainda temos uma solução para isso. A base deve ser ortonormal, então todos os vetores da base devem ter módulo igual a 1:

| u → | = 1 ⇒ α 2 ( 1 + 4 + 4 ) = 1 ⇒ 9 α 2 = 1 ⇒ 3 α = 1 ⇒ α = 1 3

| v → | = 1 ⇒ β   2 ( 4 + 1 ) = 1 ⇒ 5 β   2 = 1 ⇒ 5 β = 1 ⇒ β = 1 5

Resposta

  1. u → = 1 3 ( 1,2 , 2 )

  2. v → = 1 5 ( 2,0 , - 1 )

  3. w → = 5 15 ( 2 , - 5,4 )

Exercícios de Livros Relacionados

26. Calcular z , sabendo-se que A 2,0 , 0 , B 0,2 , 0 e C 0,0 , z são vértices de um triângulo de área 6.
27. Dados os pontos A 2,1 , - 1 e B 0,2 , 1 , determinar o ponto C do eixo O y de modo que a área do triângulo A B C seja 1,5 u.a.
29. Os pontos médios dos lados do triângulo A B C são M 0,1 , 3 , N 3 , - 2,2 e P 1,0 , 2 . Determinar a área do triângulo A B C .
25. Encontrar um vetor ortogonal ao plano determinado pelos pontos P ,Q e R e calcular a área do triângulo P Q R , dado que:a) P 3,0 , 0 ,Q ' 0,3 , 0 e R 0,0 , 2 ;b) P 2,3 , 0 ,Q 0,2 , 1 e R 2,0 , 2 .
25. Encontrar um vetor ortogonal ao plano determinado pelos pontos P ,Q e R e calcular a área do triângulo P Q R , dado que:a) P 3,0 , 0 ,Q ' 0,3 , 0 e R 0,0 , 2 ;b) P 2,3 , 0 ,Q 0,2 , 1 e R 2,0 , 2 .