Enunciado
Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 5.Exercícios Propostos - Ex. 5
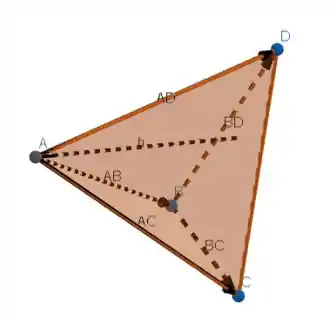
No tetraedro , temos , e . Calcule a altura do tetraedro relativa ao vértice .
Passo 1
Uma informação muito importante para a gente conseguir resolver essa questão é que a altura do tetraedro é igual a três vezes o volume dividido pela área da base pois
onde é a área da base.
Então, se soubermos o volume e a área da base, só precisamos dividir um pelo outro e multiplicar por 3 e teremos a altura. Felizmente calcular o volume é simples, só precisamos do produto misto
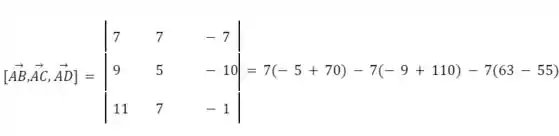
O volume do tetraedro é dado pelo módulo desse produto misto dividido por 6:
Passo 2
Beleza, já temos o volume. Mas e quanto a área da base? A base que estamos considerando é aquela que não contém o vértice A, ou seja BCD. Assim, precisamos dos seguintes vetores:
Como a base é triangular, então a sua área é metade do módulo do produto vetorial de dois vetores que representam as arestas. Não se preocupe se parece complicado, na verdade só queremos dizer
Vamos calcular o produto vetorial separadamente:
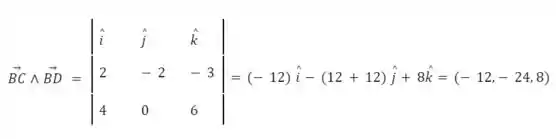
Logo,
Passo 3
Agora chegamos ao tão aguardado momento de obter a altura. Vamos substituir os resultados dos passos anteriores em