Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 5.1 - Ex. 1

Reduzir cada uma das equações de forma a identificar a cônica que ela representa e faça um esboço do seu gráfico:

  1. 4 x 2 + 2 y 2 = 1
  2. x 2 + y = 0
  3. x 2 - 9 y 2 = 9

Passo 1

E aí, tudo beleza?

Vamos lá. A gente tem que reescrever essas equações para elas ficarem da forma de uma das cônicas.

  1. 4 x 2 + 2 y 2 = 1

    2. Como já tá está igualada a 1, não precisamos dividir os termos. Mas podemos reescrever assim:

    x 2 1 4 + y 2 1 2 = 1

    x 2 1 2 2 + y 2 1 2 2 = 1

    E chegamos na equação de uma elipse, com a = 1 2   e   b = 1 2 , centrada na origem.

    Eis o esboço:

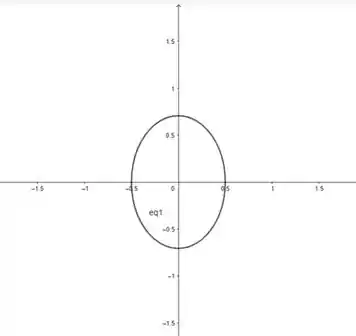
    Passo 2

  2. x 2 + y = 0

    3. Como só temos uma das variáveis elevado ao quadrado, a equação se trata de uma parábola, e podemos escrevê-la como:

    y = - x 2

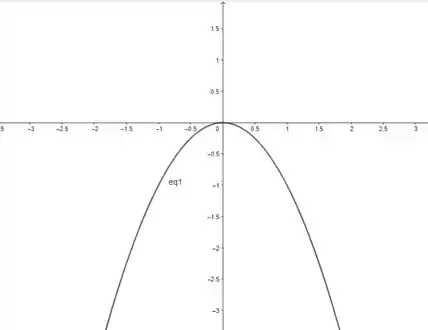
    Passo 3

  3. x 2 - 9 y 2 = 9

Aqui, para termos uma equação com 1 do lado direito, vamos dividir tudo por 9:

x 2 9 - y 2 = 1

x 2 3 2 - y 2 = 1

Essa é a equação de uma hipérbole, com a = 3 e b = 1 , centrada na origem.

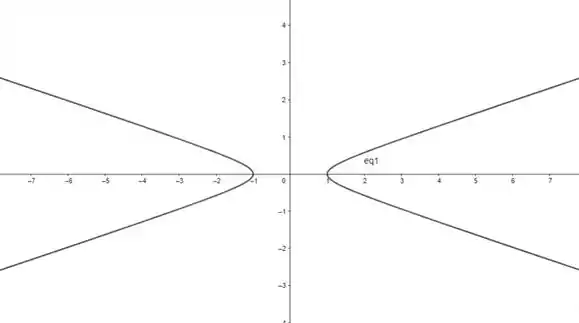
Resposta

  1. Elipse.
  2. Parábola.
  3. Hipérbole.

Exercícios de Livros Relacionados

Nos casos em que a equação dada descreve uma elipse de focos em algum dos eixos coordenados, especifique-o e calcule: a distância focal, a medida do eixo maior e a medida do eixo menor. Faça alguns es
Nos casos em que a equação dada descreve uma elipse de focos em algum dos eixos coordenados, especifique-o e calcule: a distância focal, a medida do eixo maior e a medida do eixo menor. Faça alguns es
São dados, em cada caso, o parâmetro geométrico a e os focos de uma elipse. Obtenha uma equação algébrica de segundo grau em x e y que todo ponto x , y da elipse deva satisfazer. a = 4 F 1 = - 3,2 F 2
Nos casos em que a equação dada descreve uma elipse de focos em algum dos eixos coordenados, especifique-o e calcule: a distância focal, a medida do eixo maior e a medida do eixo menor. Faça alguns es
Nos casos em que a equação dada descreve uma elipse de focos em algum dos eixos coordenados, especifique-o e calcule: a distância focal, a medida do eixo maior e a medida do eixo menor. Faça alguns es