Enunciado

Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 1.1 - Ex. 1b

(b) 2C − D

Passo 1

Bom, vamos pra mais uma questão, e essa está pedindo pra gente fazer uma multiplicação de matriz por um escalar. Vamos começar por essa parte.

Para fazermos multiplicação por um escalar, devemos multiplicar cada elemento da matriz por esse número, que no caso dessa questão é 2.

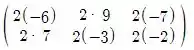
2C =

Simplificando esse valor, temos:

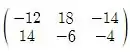
2C =

Passo 2

Já achamos o valor da matriz de 2C, agora precisamos pegar esse valor e subtrair da matriz D.

Teremos então: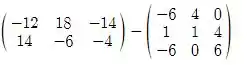

2C - D =

Temos que lembrar da regra de soma e subtração de matrizes, para conseguirmos fazer essas operações, as matrizes precisam ter as mesmas dimensões (mesmo número de linhas e colunas) e que não é o caso dessa que estamos tentando resolver.

Você notou que uma possui dimensão 2x3 e a outra 3x3, não são iguais então não é possível fazer essa operação.

Resposta

Não é possível resolver pois as dimensões das matrizes são diferentes por isso não conseguimos realizar a subtração delas.

Exercícios de Livros Relacionados

Ache números α,β de modo que os múltiplos α meβ n das matrizes abaixo sejam matrizes ortogonais. m = 2 - 2 1 1 2 2 2 1 - 2 e n = 6 3 2 - 3 2 6 2 - 6 4

Usando a matriz α m do exercício anterior, efetue uma rotação dos eixos (mudança de coordenadas mantendo a origem fixa). Ache as novas coordenadas ( x ' , y ' , z ' ) dos pontos cujas coordenadas ( x

Ainda com a rotação dos eixos dada pela matriz ortogonal α m acima, quais são, nas novas coordenadas x ' , y ' , z ' , as equações dos seguintes planos? b )2 x - 2 y + z = 3

Ainda com a rotação dos eixos dada pela matriz ortogonal α m acima, quais são, nas novas coordenadas x ' , y ' , z ' , as equações dos seguintes planos? a )2 x + y + 2 z = 1