(c) (2D − 3E )
Passo 1
Lá vamos nós novamente, nessa questão começaremos resolver dentro do parênteses e nele notamos que devemos fazer a transposta da matriz D e da matriz E mas se percebemos, fora do parênteses teremos que fazer a transposta novamente, anulando a primeira e retornando ao valor original. Então resolvermos a questão da seguinte forma:
c) 2D - 3E
E para resolvermos essa questão teremos que multiplicar as matrizes por um escalar. Vamos começar com a matriz 2D.
Devemos apenas multiplica cada elemento da matriz D pelo escalar 2:

2D =
Simplificando temos que:

2D =
Passo 2
Vamos fazer a mesma coisa agora, só que com a matriz E multiplicada pelo escalar 3:

3E =
Simplificando temos:

3E =
Passo 3
Agora para fechar essa questão vamos fazer 2D - 3E:

2D - 3E =
Analisando percebemos que eles possuem as mesmas dimensões, então é possível fazer a subtração, é só subtrairmos os elementos das posições equivalentes.

2D - 3E =
Simplificando temos:
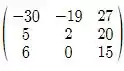
2D - 3D =
Resposta
(c) (2D − 3E ) =