Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Callioli - Álgebra Linear e Aplicações - Parte 1- Ed: 6º - Capítulo 7.4 - Ex. 4

Repetir o exercício 3 com a matriz

([[2,1,3,0],[1,2,1,0],[0,0,2,1],[3,1,1,4]])

Passo 1

Primeiro macete que é importante a gente saber, é construir nossa matriz de sinais, ou seja

([[+,-,+,-],[-,+,-,+],[+,-,+,-],[-,+,-,+]])

Que será útil para resolvemos nosso determinante pelo método do cofator.

2 , e o sinal a ele correspondente na nossa matriz ai em cima, 2 (mais). Assim multiplicamos ele pela matriz que sobra removendo a linha e a coluna que o + pertence, ou seja

2

+ 2 * d e t

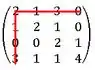
E seguindo a mesma lógica para o novo determinante, teremos

+ 2 * det ([[2,1,0],[0,2,1],[1,1,4]])

+ 2 * (+ 2 * det ([[2,1],[1,4]]) - 1 * det ([[0,1],[1,4]]) + 0 * det ([[0,2],[1,1]]))

= + 2 * (+ 2 * (8 - 1) - 1 * (- 1) + 0 * det (- 2))

Passo 2

O passo 1 fizemos a conta para o primeiro cofator. Agora se seguimos a mesmas lógicas, teremos que para o segundo cofator teremos

- 1 * det ([[1,1,0],[0,2,1],[3,1,4]]) = - 1 * (1 * det ([[2,1],[1,4]]) - 1 * det ([[0,1],[3,4]]) + 0 * det ([[0,2],[3,1]]))

= - 1 * ((8 - 1) - (- 3)) = - 1 (7 + 3) = - 10

Para a terceira temos

+ 3 * det ([[1,2,0],[0,0,1],[3,1,4]]) = + 3 * (1 * det ([[0,1],[1,4]]) - 2 * det ([[0,1],[3,4]]) + 0 * det ([[0,0],[3,1]]))

+ 3 * ((- 1) - 2 * (- 3) + 0) = + 3 * (- 1 + 6) = 15

E a ultima linha como podemos ver, o cofator é zero, logo os termos que vem de lá.

Passo 3

Então temos que o determinante será

det (A) = 30 - 10 + 15 = 35

Resposta

det (A) = 35

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular o cofator do elemento x da matrizA = ([[[[[[0,1]],[[0,3]]]]],[[[[[1,2]],[[1,1]]]]],[[[[[2,1]],[[0,0]]]]],[[[[[3,x]],[[2,1]]]]]])
Calcule os cofatores de cada um dos termos da matriz A = 1 2 1 0 1 2 2 3 1
Desenvolva pela primeira coluna det ⁡ A = ∑ i = 1 3 a i 1 A i 1 e depois calcule o determinante da matriz 3 4 0 1 1 0 2 0 2
Sejam A , B e C matrizes de ordem 2 e seja X = A C 0 B De ordem 4. Provar que det ⁡ X = det ⁡ A det ⁡ B . Este resultado vale para A , B , C ∈ M n R .