Desenvolva pela primeira coluna e depois calcule o determinante da matriz
Passo 1
Primeiro macete que é importante a gente saber, é construir nossa matriz de sinais, ou seja
Que será útil para resolvemos nosso determinante pelo método do cofator.
Assim podemos resolver nosso determinante da seguinte maneira: Tome o primeiro valor do nosso determinando, , e o sinal a ele correspondente na nossa matriz ai em cima, (mais). Assim multiplicamos ele pela matriz que sobra removendo a linha e a coluna que o pertence, ou seja
O próximo valor pegamos o e o sinal a ele correspondente, (menos), assim ficamos com
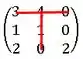
E por último teremos o valor e o seu sinal positivo.
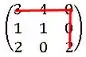
Passo 2
Assim temos que
O nosso determinante.