Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 6.Problemas propostos - Ex. 31h
31. Representar graficamente os planos de equações:
h)
Passo 1
Então galera, antes de representarmos graficamente os planos de equações vamos nos lembrar de qual é a expressão geral do plano, tudo bem? Assim como estudado no capítulo em questão do Winterle, temos que a expressão geral do plano é essa aqui ó:
Onde os coeficientes das coordenadas, ou seja, são as componentes de um vetor normal ao plano, mas isso não irá implicar em nada na nossa resolução. Para representarmos graficamente o plano de equações que nos foi dado, devemos atribuir valores arbitrários, mas convenientes, para nossas variáveis , e , a fim de obter pontos pertencentes ao plano.
Parece confuso? Prometo que não é! Vem comigo!
Passo 2
A equação que nos foi dada é:
Se adotarmos , teremos:
Então um dos pontos é , que basicamente é a origem do sistema de coordenadas. Agora adotando , teremos:
Então outro ponto é , que também é a origem do sistema de coordenadas. Como , então nosso plano terá que ser um tipo de plano identidade, que passa pela origem e pelos quadrantes ímpares do plano . Marcando esses pontos e esboçando o plano, teremos algo assim:
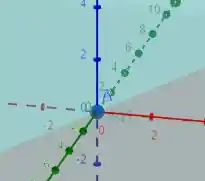
No qual o eixo vermelho é , o eixo verde é e o eixo azul é . Ademais, o plano é essa região azul transparente que passa por e no gráfico, que é exatamente o plano discutido aqui em cima na resolução.
Resposta
Representação do plano:
