Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 8.Problemas Propostos - Ex. 3f
Representar graficamente as seguintes superfícies cilíndricas:
Passo 1
O livro considera que se pensarmos em uma superfície cilíndrica cuja diretriz é uma curva que se encontra num dos planos coordenados e a geratriz é uma reta paralela ao eixo coordenado não contido no plano. Neste caso, a equação da superfície cilíndrica é a mesma de sua diretriz. Por exemplo, se a diretriz for a parábola :
A equação da superfície cilíndrica também será:
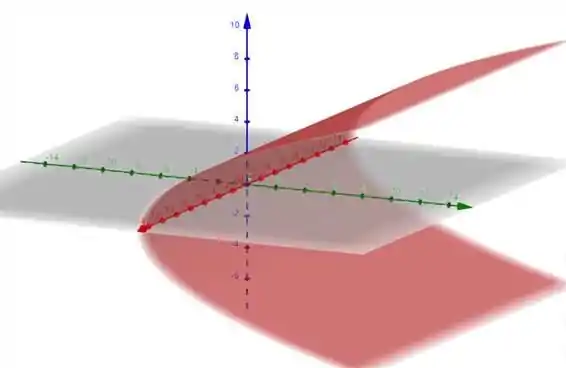
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Reduzir cada uma das equações à forma canônica (caso não esteja), identificar a superfície e construir seu gráfico. 4 x 2 - y 2 + 2 z 2 + 4 = 0
Reduzir cada uma das equações à forma canônica (caso não esteja), identificar a superfície e construir seu gráfico. z 2 - 4 x 2 - 4 y 2 = 4
Reduzir cada uma das equações à forma canônica (caso não esteja), identificar a superfície e construir seu gráfico. 3 6 x 2 + 16 y 2 - 9 z 2 - 144 = 0
7. Identificar as superfícies definidas pelas equações, dizendo ao longo de que eixo elas ocorrem, conforme o caso. k )x 2 + z - 9 = 0
7. Identificar as superfícies definidas pelas equações, dizendo ao longo de que eixo elas ocorrem, conforme o caso. d )y = 16 x 2 + 4 z 2