Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 9.Problemas propostos - Ex. 5f
Reduzir cada uma das equações à forma canônica (caso não esteja), identificar a superfície e construir seu gráfico.
Passo 1
Fala meus consagrados, tudo na boa?
O primeiro passo para reduzir uma equação na forma canônica é fazer com que o valor contido no segundo termo da igualdade seja .
Sendo a nossa equação:
Dividimos tudo por :
Simplificando:
O próximo passo é analisar as fórmulas propostas pelo livro no capítulo 9 e fazer uma comparação superficial, para dizer qual o tipo da nossa equação.
Passo 2
De acordo com o capítulo 9, nós temos aqui a equação de um Hiperboloide de duas folhas. Quando dois termos são negativos e um termo é positivo:
Dessa forma, nossa equação:
Trata-se de um hiperboloide de duas folhas com ; e . Já temos tudo, agora é só montar o gráfico.
Passo 3
Os termos e são referentes a coordenada em que a elipse se encontra em cada um dos eixos. Isso significa que montaremos um gráfico em que ,, que são como se fossem “raios” em cada um dos eixos.
Usando uma calculadora gráfica, como é o caso do Geogebra (online), teremos a seguinte superfície:
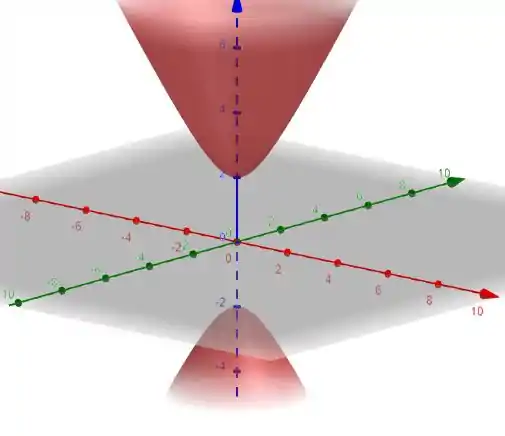
Tranquilo?
Resposta
Hiperboloide de duas folhas,