Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 9.Problemas propostos - Ex. 7k
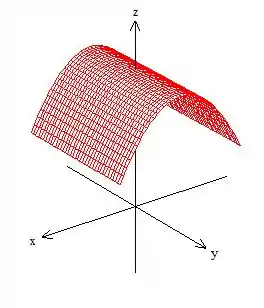
7. Identificar as superfícies definidas pelas equações, dizendo ao longo de que eixo elas ocorrem, conforme o caso.
Passo 1
Fala aí! Nesse exercício daqui estaremos trabalhando a seguinte equação:
POXA! Eu não sei se você está com as mesmas impressões que eu, mas se estiver, vai estar desconfiado de que esta equação nos representa um cilindro ao redor de (já que nem tem na equação). Vamos ver se é isso mesmo?
Passo 2
Repare que podemos isolar em função de todo mundo...
Poxa, essa equação no plano , nada mais é do que uma parábola decrescente que passa por , quando :
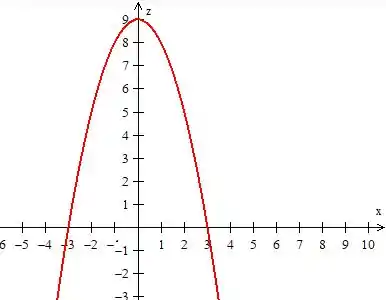
Como a equação não envolve , é porque de fato se trata de um cilindro ao redor de (basta pegar essa curva e puxar ao redor de ):
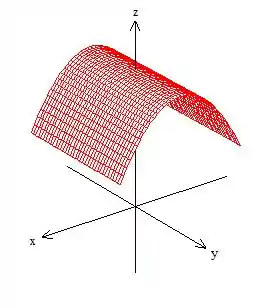
Resposta
Cilindro ao redor do eixo :
Exercícios de Livros Relacionados
Determine representações paramétricas para as seguintes superfícies.b) z = - x 2 a 2 + y 2 b 2
Determine representações paramétricas para as seguintes superfícies.c) z 2 = x 2 a 2 + y 2 b 2
Encontre uma equação em coordenadas esféricas da superfície cuja equação em coordenadas cartesianas é dada. c) x 2 + y 2 = 9
Determine representações paramétricas para as seguintes superfícies.a) - x 2 a 2 + y 2 b 2 - z 2 c 2 = 1
Mostre que a cúbica retorcida x = t, y = t 2 e z = t 3 está contida no cilindro de equação y = x 2 .