Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 9.Problemas propostos - Ex. 7d

7. Identificar as superfícies definidas pelas equações, dizendo ao longo de que eixo elas ocorrem, conforme o caso.

Passo 1

Fala aí! Nesse exercício daqui estaremos trabalhando a seguinte equação:

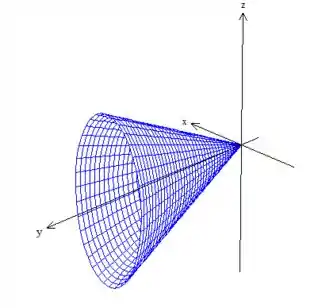
POXA! Eu não sei se você está com as mesmas impressões que eu, mas se estiver, vai estar desconfiado de que esta equação nos representa um cone elíptico (ou pelo menos um pedaço dele). Vamos ver se é isso mesmo?

Passo 2

Sabemos pela teoria, que a equação do cone elíptico (ao redor do eixo ) pode ser dada pela equação geral:

A nossa equação é parecida:

Todavia, ela só pega aparte positiva do cone em . Além disso, por curiosidade, podemos encontrar e passando como (apenas um truque matemático kkkk):

OBS: Observe que se cortarmos transversalmente o cone, temos uma elipse e essa elipse é achatada em , já que é maior que ! É sempre bom desenhar colocando esses detalhes ;)

Resposta

Parte positiva de um cone ao redor do eixo :

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dadas as equações da curva diretriz e um vetor paralelo as retas geratrizes determine a equação da superfície cilíndrica. b) x 2 + z 2 = 1 ,y = 0eV = ( 2 , 1 , - 1 )

Dadas as equações da curva diretriz e um vetor paralelo as retas geratrizes determine a equação da superfície cilíndrica. c) x 2 - y 2 = 1 ,z = 0eV = ( 0 , 2 , - 1 )

Dadas as equações da curva diretriz determine a equação da superfície cônica que tem vértice na origem O = (0, 0, 0).b) x z = 1ey = 1

Dadas as equações da curva diretriz e um vetor paralelo as retas geratrizes determine a equação da superfície cilíndrica. a) y 2 = 4 x ,z = 0eV = ( 1 , - 1,1 )

Dadas as equações da curva diretriz e um vetor paralelo as retas geratrizes determine a equação da superfície cilíndrica. d) 4 x 2 + z 2 + 4 z = 0 ,y = 0eV = ( 4 , 1 , 0 )