Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento geométrico - Ex. 7d
Dados três pontos A,B e C não colineares, como na Figura 1.31, representar o vetor nos casos:
d)
Passo 1
Primeiro vamos descobrir quem são esses vetores
Para achar o vetor , é o vetor que começa no ponto A e vai até o ponto B, assim:
Então, é só pegar a metade desse vetor:
Agora para encontrar o vetor vamos fazer primeiro o vetor , que é o vetor que começa em C e vai até B multiplicado por 2. Ele fica assim:
Para achar o vetor é só inverter o sentido do vetor que acabamos de achar
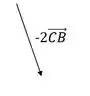
Passo 2
Somar os vetores que o enunciado pede para encontrar o vetor
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Considere os pontos P tais que a distância de P a A ( - 1,5 , 3 ) seja o dobro da distância de P a B 6,2 , - 2 . Mostre que o conjunto desses pontos é uma esfera e determine seu raio e centro.
O hemisfério superior sólido da esfera de raio 2 centrada na origem.
Escreva inequações para descrever a região dada.34. O cilindro sólido que está sobre ou abaixo do plano z = 8 e sobre ou acima do disco no plano x y com centro na origem e raio 2 .
Determine o volume do sólido que está contido em ambas as esferas x 2 + y 2 + z 2 + 4 x - 2 y + 4 z + 5 = 0 E x 2 + y 2 + z 2 = 4
A região constituída em todos os pontos entre (mas não sobre) as esferas de raio r e R centradas na origem, onde rR .