A, B, C e D são os vértices de um paralelogramo. Tem-se: A B → = C D → , C E → = 1 3 C D → , C F → = 1 2 C A → , A G → = 1 2 A B → , x → = E F → , y → = E G → e z → = E B → .Escreva x → , y → e z → em função de A B → e A C → Escreva z → em função de x → e y → .

x → = - 1 3 A B → - 1 2 A C → , y → = 1 6 A B → - A C → , z → = 2 3 A B → - A C → z → = - 6 5 x → + 8 5 y →

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 17

A, B, C e D são os vértices de um paralelogramo. Tem-se: , , , , , e .

Escreva , e em função de e

Escreva em função de e .

Passo 1

Vamos começar essa questão analisando as informações do enunciado. quer dizer que existem dois vetores com origem em C, um indo até D () e outro até um terço do caminho () e chegando no ponto E. Então E está a um terço do caminho entre C e D. Algo parecido ocorre com mas, nesse caso, o ponto F está a metade do caminho entre C e A. Do mesmo modo, indica que G está a metade do caminho entre A e B. Tudo tranquilo até agora? Então, podemos marcar os pontos E, F e G no paralelogramo e também os vetores ligando eles. Vai ficar mais ou menos assim:

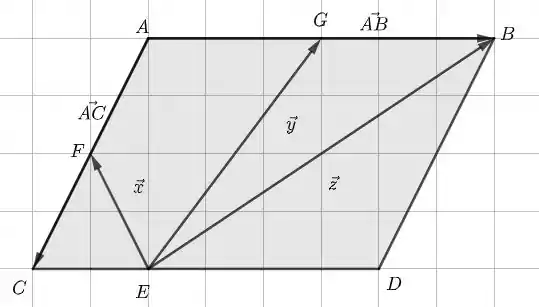
Antes de calcular os vetores , e , temos que notar que, como e , então . E lembre também que e porque vamos precisar desses resultados. Para obter , podemos ir de E a F pelo caminho ECF. Nesse caso

O vetor sai de E até G, mas também podemos escolher o caminho ECAG. Nesse caso,

Já o vetor sai de E até B. Podemos escolher o caminho EGB, por exemplo:

Passo 2

Para escrever em função de e , vamos fazer , obter um sistema de equações e resolver esse sistema:

Vamos multiplicar a primeira equação por seis e a segunda por :

Agora, somamos as duas equações e obtemos

Substituindo esse resultado na primeira equação, obtemos:

Logo,

Resposta

Exercícios de Livros Relacionados

No trapézio ABCD, B C → =v → , A D → = 2v → e E é o ponto de interseção das diagonais A C → e B D→ . Sendo B E → = λB D → , determine λ .

ABCD é um paralelogramo de diagonais A C → e B D → . O ponto R é tal que 3 D R → = 2 C D → e S é tal que 2 B S → = S C → .Marque R e S na figura.Escreva R S → em termos de A B → e A D → .

Os pontos A, B, C e D são vértices consecutivos de um paralelogramo. A B→=x→ , A D→=y→ , A P→=1 3 x→ , A Q→= 3 4y→ e F é a interseção de P Q→ e A C→ . Escreva Q F→ em função de x→ e y→ .

Num triângulo ABC temos 3 B P → = 4 P C → e 3 P Q → = 4 Q A → . Localize na figura os pontos P e Q, justificando a resposta.A seguir, expresse A P → e B Q → como combinações lineares de u → = A B → e