Enunciado
Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 22
No trapézio ABCD, , e E é o ponto de interseção das diagonais e . Sendo , determine .
Passo 1
Fala, galerinha! Espero que estejam animados para mais uma questão.
O enunciado da questão já nos diz que . Mas também temos que notar que . Daqui a pouco você vai entender porque vamos precisar dessa propriedade. A partir da primeira propriedade, obtemos
Passo 2
Seguindo as informações do enunciado, podemos desenhar a seguinte figura:
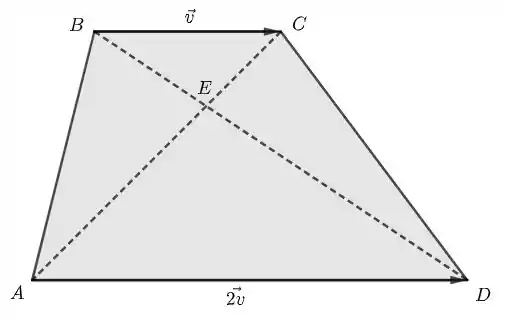
Na figura acima, fica claro que
Passo 3
Nos itens anteriores, nós obtivemos de duas formas, que devem ser iguais. Logo,
Como e não são paralelos, a igualdade acima só vai ser verdadeira se ambos os lados forem nulos. Para que isso aconteça, é necessário que
Resposta
Exercícios de Livros Relacionados
Se os vetores u ,vew não são coplanares, mostre geometricamente que todo vetor do espaço se exprime como combinação linear
Dados quatro vetores no espaço, prove que um deles é combinação linear dos outros três.
Determine quais dos seguintes conjuntos é tal que nenhum dos seus vetores é combinação linear dos outros dois: a ){ ( 1 ,- 1 ,2 ) , ( 1 ,1 ,0 ) , ( 1 ,- 1 ,1 ) } b ){ ( 2 ,1 ,2 ) , ( 1 ,- 1 ,1 ) , ( 5
Sejam r 1={ A+s·v ;s∈R }er 2={ B+t·w ;t∈R } duas retas:i) Prove que r 1=r 2 se, e somente se, os vetores A B → e w são múltiplos de v .ii) Prove que r 1er 2 são coplanares se, e somente se, os vetores
Sejam A, B, C, D pontos não-coplanares. Descreva um método geométrico (isto é, sem uso de coordenadas) que permita escrever, para qualquer ponto P, o vetor A P → como combinação linear dos vetores u =