Enunciado
Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 21
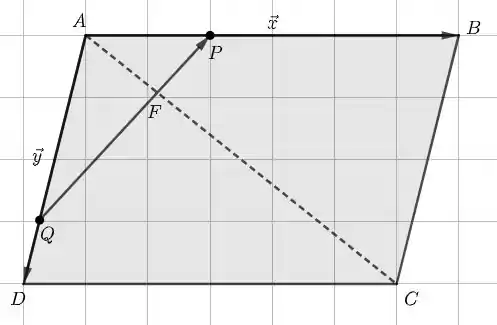
Os pontos A, B, C e D são vértices consecutivos de um paralelogramo. , , , e F é a interseção de e . Escreva em função de e .
Passo 1
A questão pede para escrever em função de e . A maneira de fazer isso é partir do fato de que deve ser proporcional a porque os dois vetores têm direção e sentido. Assim,, , e temos que determinar . Na figura abaixo, vemos que
Logo,
Passo 2
Também podemos obter pelo caminho QAF:
Não temos como saber exatamente quanto é em termos de e , mas sabemos que deve ser proporcional a , ou seja, . O vetor , por outro lado, pode ser determinado. Para tanto, temos que notar que porque esses dois vetores têm o mesmo módulo, direção e sentido. Belezinha até aqui? Continuando o raciocínio, podemos escrever como
Então, e
Passo 3
Nos passos anteriores, obtivemos de duas formas diferentes, mas que devem ser iguais no final das contas. Isso quer dizer que
Sabemos que e não são paralelos. Então, a única maneira do resultado acima ser verdadeiro, é se tivermos um vetor nulo em ambos os lados. e também não são nulos, então a única opção restante é que os coeficientes sejam nulos:
Substituindo esse valor na expressão encontrada no Passo 1, obtemos