ABCD é um paralelogramo de diagonais e . O ponto R é tal que e S é tal que .
- Marque R e S na figura.
- Escreva em termos de e .
Passo 1
- Fala, galerinha! Mais uma questão para a gente detonar. Vamos começar interpretando os dados do enunciado: significa que os vetores e são paralelos. Além disso começa em C e termina em D enquanto começa em D e termina em R. Isso indica que R está fora do paralelogramo. Enquanto isso, indica que S está exatamente entre B e C porque termina em S e começa em S. Além disso,
- Agora queremos escrever em termos de e . Como a figura é um paralelogramo, as distâncias AB e CD são iguais, além do fato desses segmentos serem paralelos. Então, e tem o mesmo módulo, direção e sentido. Isso quer dizer que , o que vai facilitar bastante os nossos cálculos. O mesmo é válido para e : . Na figura acima, podemos notar que
Assim, vemos que tem dois terços do tamanho de enquanto S está a um terço da distância entre B e C. Com essas informações, podemos desenhar um paralelogramo, identificar os pontos R e S e o vetor ligando os dois:
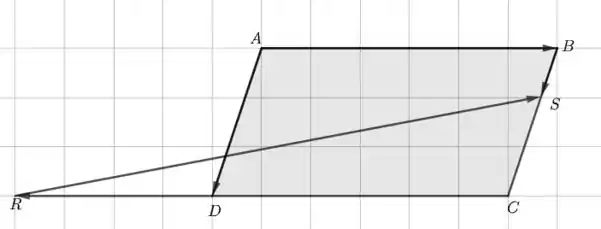
Passo 2
onde usamos os resultados encontrados no Passo 1. Agora, lembrando que e , nós podemos obter
.