Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 14

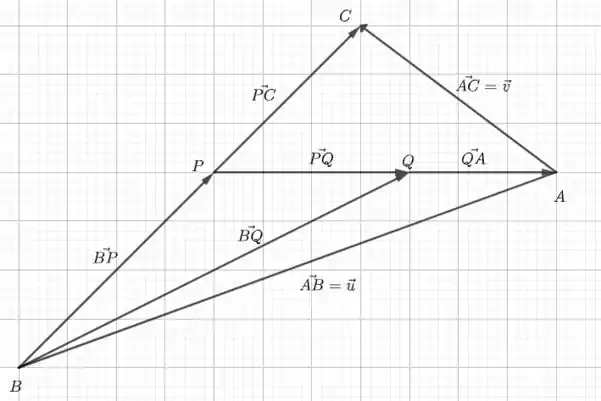
Num triângulo ABC temos 3 B P → = 4 P C → e 3 P Q → = 4 Q A → .

  1. Localize na figura os pontos P e Q, justificando a resposta.
  2. A seguir, expresse A P → e B Q → como combinações lineares de u → = A B → e v → = A C → .

Passo 1

  1. Fala pessoal! Vamos partir para mais uma questão? O enunciado diz que 3 B P → = 4 P C → , então esses dois vetores são paralelos mas não tem a mesma origem. Logo, o ponto P está entre B e C. Agora nós temos que refletir sobre a relação 3 P Q → = 4 Q A → . Temos que notar que P Q → + Q A → = P A → , ou seja, o ponto Q está na linha que une P e A. Além disso, temos

    2. B C → = B P → + P C → = B P → + 3 4 B P → = 7 4 B P →   ⇒ B P → = 4 7 B C → ⇒ P C → = 3 4 B P → = 3 4 4 7 B C → = 3 7 B C →

    P A → = P Q → + Q A → = P Q → + 3 4 P Q → = 7 4 P Q → ⇒ P Q → = 4 7 P A → ⇒ Q A → = 3 7 P A →  

    Então P está a 4 7 do caminho entre B e C e Q está a 4 7 do caminho entre P e A. O desenho fica mais ou menos como na imagem abaixo, lembrando que o formato do triângulo não importa porque só precisamos da figura para visualizar como os vetores estão relacionados entre si.

    Passo 2

  2. Agora vamos calcular A P → e B Q → como combinações lineares de u → = A B → e v → = A C → :

A P → = A C → + C P → = A C → - P C → = A C → - 3 7 B C → = A C → - 3 7 ( B A → + A C → ) = 3 7 B A → + 4 7 A C → = 3 7 u → + 4 7 v →

Para B Q → , vamos levar em consideração a figura abaixo. Podemos notar que

B Q → = B A → + A Q → = - A B → - Q A → = - A B → - 3 7 P A → = - A B → + 3 7 A P → = - u → + 3 7 3 7 u → + 4 7 v →

B Q → = - u → + 9 49 u → + 12 49 v → = 9 - 49 49 u → + 12 49 v → = - 40 49 u → + 12 49 v →

Resposta

A P → = 3 7 u → + 4 7 v →

B Q → = - 40 49 u → + 12 49 v →

Exercícios de Livros Relacionados

Seja A 1 A 2 A 3 A 4 A 5 A 6 um hexágono de centro O. Escreva A 1 A i → , i = 2 , . . . , 6 em função de a → = A 1 A 2 → e b → = A 1 A 6 → .Mostre que ∑ i = 2 6 A 1 A i → = 6 A 1 O → .Expresse w → = A
No trapézio ABCD ao lado, temos A B → = 3 u → , C D → = 2 u → , A D → = v → , A C → = a → , A S → = b → e D R → = c → . Sendo R e S os pontos de trissecção do lado BC, Escreva a → , b → e c → em funçã
Demonstre: Em um quadrilátero qualquer ABCD, os pontos médios M, N, P e Q dos lados são vértices de um paralelogramo.
Dados os vetores O A→ = a→ , O B→ = b→ e O C→ = c → tais que 2 A B →-3 B C →+ A C →=0 → , prove que os vetores a→ , b→ e c→ são l.d..
O A →=( 4,1 , - 3 ) , O B →=( 2 , - 1,1 ) , A D → é paralelo a ( 2 , x , 0 ) e D está alinhado com O e B. Determine A D → .