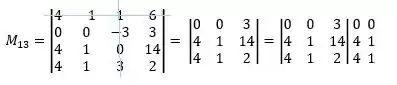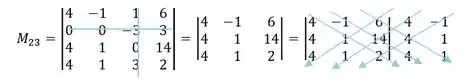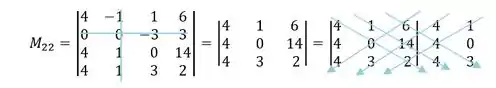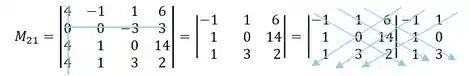3. Seja
A = [[[4,-,1,,,,1,,,,6],[0,,,,0,-,3,,,,3],[4,,,,1,,,,0,,,14],[4,,,,1,,,,3,,,,2]]]
Encontre
(a)
M_13
e
C_13
(b)
M_23
e
C_23
(c)
M_22
e
C_22
(d)
M_21
e
C_21
Passo 1 Para obter os menores da matriz
A
, temos que recordar que “O menor de uma entrada
a_i j
” denotado por
M_i j
, é simplesmente o determinante da matriz que sobra quando retiramos uma linha
i
e coluna
j
.
E para calcular o cofator é só aplicar a seguinte fórmula:
C_i j = (- 1)^(i + j) M_i j
.
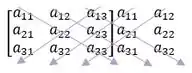
Podemos calcular o determinate de uma matriz 3x3 de maneira mais simples, com esse método:
Passo 2 (a)
M_13
e
C_13
M_13 = [(0 xx 1 xx 2) + (0 xx 14 xx 4) + (3 xx 4 xx 1)] - [ (3 xx 1 xx 4) + (0 xx 1 4 xx 1) + (0 xx 4 xx 2) ]
M_13 = [ 0 + 0 + (12) - [ 12 + 0 + 0 ]
M_13 = 12 - (12) = 0
C_13 = (- 1)^(1 + 3) M_13 = 1 xx M_13 = M_13 = 0
Passo 3 (b)
M_23
e
C_23
M_23 = [(4 xx 1 xx 2) + (- 1 xx 14 xx 4) + (6 xx 4 xx 1)] - [ (- 1 xx 4 xx 2) + (4 xx 14 xx 1) + (6 xx 1 xx 4) ]
M_23 = [ 8 + ( - 56 ) + 24 ] - [ ( - 8 ) + 56 + 24 ]
M_23 = - 24 - 72 = - 96
C_23 = (- 1)^(2 + 3) M_23 = - 1 xx M_23 = - M_23 = 96
Passo 4 (c)
M_22
e
C_22
M_22 = [(4 xx 0 xx 2) + (1 xx 14 xx 4) + (6 xx 4 xx 3)] - [ (1 xx 4 xx 2) + (4 xx 14 xx 3) + (6 xx 0 xx 4) ]
M_22 = [ 0 + 56 + 72 ] - [ 8 + 168 + 0 ]
M_22 = 128 - 175 = - 48
C_22 = (- 1)^(2 + 2) M_22 = 1 xx M_22 = M_22 = - 48
Passo 5 (d)
M_21
e
C_21
M_21 = [(- 1 xx 0 xx 2) + (1 xx 14 xx 1) + (6 xx 1 xx 3)] - [ (1 xx 1 xx 2) + (- 1 xx 14 xx 3) + (6 xx 0 xx 1) ]
M_21 = [ 0 + 14 + 18 ] - [ 2 + (- 42) + 0 ]
M_21 = 32 - ( - 40 ) = 72
C_21 = (- 1)^(2 + 1) M_21 = - 1 xx M_21 = - M_21 = - 72
Resposta (a)
M_13 = 0
C_13 = 0
(b)
M_23 = - 96
C_23 = 96
(c)
M_22 = - 48
C_22 = - 48
(d)
M_21 = 72
C_21 = - 72
MOSTRAR SOLUÇÃO COMPLETA
Ver Outros Exercícios desse livro