Enunciado
Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 28
Seja ABC um triângulo qualquer com medianas , e . Demonstre que
Passo 1
Antes de começar essa questão, temos que lembrar a definição de mediana. Mediana é uma reta que sai de um dos vértices até o ponto médio localizado no na aresta oposta. Parece complicado? Talvez uma figura ajude com a visualização:
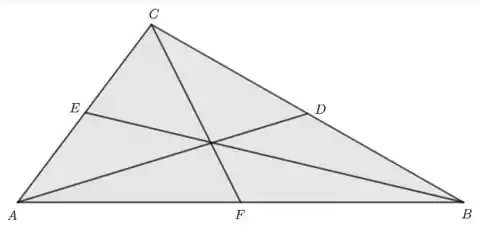
Então, , e são as medianas do triângulo.
Passo 2
Para demonstrar que , vamos utilizar o resultado do Exercício Resolvido 3 que relaciona a mediana com os outros dois vetores saindo do vértice. Assim, vamos escrever cada mediana em termos de :
Assim, a soma das medianas será:
.
Resposta
Ver a resolução acima.
Exercícios de Livros Relacionados
Seja G o baricentro (ponto de encontro das medianas) do triângulo ABC. Prove que G A → + G B → + G C → = 0 .
Fixando uma reta r , indiquemos com v ' a projeção ortogonal de um vetor arbitrário v sobre r . Prove as seguintes propriedades:b) v ' ' = v '
Sejam u = O P → ,v = O Q → vetores não nulos tais que u v + v u = O R → também seja diferente de zero. Prove que O R é a bissetriz do ˆangulo P Ô Q Ô . Obtenha, a partir daí, a inclinação dessa bisset
Indicando genericamente por v * o vetor obtido de v por rotação positiva de 90◦, prove que α u + β v * = α u * + β v *eu , v *+u * , v =0 para quaisquer vetores u , v do plano e α ,β ∈ R .
Sejam A, B e C pontos do plano. Prove que as seguintes afirmações são equivalentes: a )A B → , A C → =A B → 2