Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear e Aplicações (Reginaldo J. Santos)- Ed: 1º - Capítulo 2.1 - Ex. 4

Seja V =   C 0 - 1,1 o conjunto das funções contínuas no intervalo - 1,1 em R com o produto interno definido por: < f , g >   =   ∫ - 1 1 f t g t d t

a) Mostre que o conjunto 1 ,   t ,   t 2 , … , t n , … , não é ortogonal.

b) Mostre que f 1 t = t e f 2 t = t ² são ortogonais e verifique a validade do Teorema de Pitágoras para f 1 t = t e f 2 t = t ²

c) Calcule a projeção de t 5 em t . Faça um esboço dos gráficos de t 5 e p r o j t t 5 no mesmo sistema de coordenadas.d) Escreva t 5 como uma soma de dois polinômios ortogonais p 1 ( t ) e p 2 ( t ) sendo p 1 ( t ) um múltiplo escalar de t .e) Determine o ângulo θ entre t e t 5 .

Passo 1

E aí galerinha!! Beleza? Aqui temos uma questão bem bacana de Álgebra Linear, vamos lá?

Vamos separar as condições, para a nossa resolução ficar mais fácil:

< f , g >   =   ∫ - 1 1 f t g t d t

Passo 2

Pessoal, vamos resolver o primeiro questionamento do exercício, que pede: mostre que o conjunto 1 ,   t ,   t 2 , … , t n , … , não é ortogonal.Foi nos dado uma equação genérica, então podemos escolher de forma arbitrária quaisquer valores que quisermos, ok?Vamos escolher as funções t   e   t ³ , depois substituiremos ela na integral, para provar que não ortogonal a mesma tem que ser ≠ 0 . < t , t 3 >   = ∫ - 1 1 t ∙ t ³ d t Resolvendo essa integral, chegaremos em um resultado de 2 5 ≠ 0 provando que a nossa função não é ortogonal.

Passo 3

Bom pessoal, iremos para o segundo questionamento do exercício que diz: mostre que f 1 t = t e f 2 t = t ² são ortogonais e verifique a validade do Teorema de Pitágoras para   f 1 t = t e f 2 t = t ²

Primeiramente iremos substituir os dados nesse questionamento em nossa função genérica que foi dada para nós: < f , g >   =   ∫ - 1 1 f t g t d t

< f 1 , f 2 >   =   < t , t 2 >   = ∫ - 1 1 t ∙ t ² d t

< f 1 , f 2 >   =   < t , t 2 >   = ∫ - 1 1 t 3 d t = 0

Agora, vamos calcular a norma da função acima: < f 1 , f 2 >   =   < t , t 2 >   = ∫ - 1 1 t 3 d t = 0

| |   f 1 | | 2 + | |   f 2 | | 2   =   | |   t | | 2 , | |   t ² | | 2 =   < t , t > +   < t 2 , t 2 >  

| |   f 1 | | 2 + | |   f 2 | | 2 =   ∫ - 1 1 t 2 d t +   ∫ - 1 1 t 4 d t R e s o l v e n d o   e s s a   i n t e g r a l ,   c h e g a m o s   n e s s e   r e s u l t a d o :  

| |   f 1 | | 2 + | |   f 2 | | 2 =   16 15 A g o r a ,   v a m o s   resolver, utilizando o Teorema de Pitágoras, lembrando que para verificarmos a validade, o mesmo tem que resultar no valor da integral que chegamos acima, se não todo o nosso esforço foi em vão, vamos lá! | |   f 1 + f 2   | | 2 = | |   t + t ²   | | 2 =   < t + t 2 , t + t ² >

| |   f 1 + f 2   | | 2 = ∫ - 1 1 t + t 2 2 d t

Resolvendo essa integral, chegamos em:

| |   f 1 + f 2   | | 2 = 16 15 Portanto, o Teorema de Pitágoras tem a sua validade!

Passo 4

Continuando a nossa saga, vamos para o próximo questionamento do exercício, em que nos diz: calcule a projeção de t 5 em t . Faça um esboço dos gráficos de t 5 e p r o j t t 5 no mesmo sistema de coordenadas.

Beleza, vamos calcular a projeção utilizando a seguinte fórmula: p r o j t t 5 = < t 5 ,   t > | |   t   | | 2 t p r o j t t 5 = < t 5 ∙   t > | |   t   | | 2 t

Substituindo:

p r o j t t 5 = ∫ - 1 1 t 6 d t ∫ - 1 1 t 2 d t t

Resolvendo a integral, chegaremos em:

2 7 2 3 t

2 7 ∙ 3 2 t

3 7 t

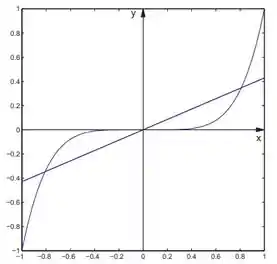Agora, realizaremos o esboço do gráfico, é apenas um esboço. Ok pessoal, não precisa ser nada muito profissional!

Passo 5

Já estaaaaaaaaaaaaaaaaaaaaamos, quase acabando, falta pouco e o próximo questionamento é muito simples, o exercício pede que: escreva t 5 como uma soma de dois polinômios ortogonais p 1 ( t ) e p 2 ( t ) sendo p 1 ( t ) um múltiplo escalar de t .Para esse exercício, vamos utilizar o resultado no passo 4 que será muito útil para nós, que tal escrevermos um polinômio genérico para nos auxiliar? t 5 = t 5 - x t + x t Esse polinômio, eles nos traz justamente o que encontramos no passo 4, agora é só substituir os dados e correr pro abraço!

t 5 = t 5 - x t + x t

t 5 = t 5 - 3 7 t + 3 7 t

Prontinho, temos a nossa soma de dois polinômios, olha que fácil!

Passo 6

Finaaaaaaaaaaaaaaaaalmente, chegamos no último questionamento do exercício, que nos diz: determine o ângulo θ entre t e t 5 .

Determinaremos o ângulo pela seguinte equação: cos ⁡ θ = < t 5 ,   t > | |   t 5 | |   ∙ | |   t 2 | |  

Agora, vamos nessa:

cos ⁡ θ = < t 5 ,   t > | |   t 5 | |   ∙ | |   t 2 | |  

cos ⁡ θ = < t 5 ∙   t > | |   t 5 | |   ∙ | |   t 2 | |  

cos ⁡ θ = ∫ - 1 1 t 6 d t ∫ - 1 1 t 10 d t   ∙ ∫ - 1 1 t 2 d t  

cos ⁡ θ = 2 7 2 11   ∙ 2 3   ∙

cos ⁡ θ = 3 7

θ = a r c o s   3 7

θ = 35 °

Quanto trabalho né? Mas deu ceeeeeerto!

Essa resolução te ajudou? Responde Aí! Até a próxima, tchaaaaau!!

Resposta

Resposta no passo 2

| |   f 1 | | 2 + | |   f 2 | | 2 = | |   f 1 + f 2   | | 2 = 16 15

3 7 t

Resposta no passo 4 (Gráfico)

t 5 = t 5 - 3 7 t + 3 7 t

θ = 35 °

Exercícios de Livros Relacionados

3. Em cada parte, determine se a matriz é ortogonal. Se for, obtenha a inversa.(a) 1 0 0 1 (b) 1 2 - 1 2 1 2 1 2 (c) 0 1 1 2 1 0 0 0 0 1 2 (d) - 1 2 1 6 1 3 0 - 2 6 1 3 1 2 1 6 1 3 (e) 1 2 1 2 1 2 1 2
5. Verifique que as matrizes de reflexão nas Tabelas 1 e 2 da Seçao 4.9 são orgtonais.
3. Em cada parte, determine se a matriz é ortogonal. Se for, obtenha a inversa.(a) 1 0 0 1 (b) 1 2 - 1 2 1 2 1 2 (c) 0 1 1 2 1 0 0 0 0 1 2 (d) - 1 2 1 6 1 3 0 - 2 6 1 3 1 2 1 6 1 3 (e) 1 2 1 2 1 2 1 2
14. Seja W a reta em R 2 de equação y = 2 x . Obtenha uma equação para W ⊥ .
13. Suponha que R 4 tenha o produto interno euclidiano e seja u = - 1,1 , 0,2 . Determine se o vetor u é ortogonal ao subespaço gerado pelos vetores w 1 = ( 1 , - 1,3 , 0 ) e w 2 = 4,0 , 9,2 .