Seja T = h , k um ponto da hipérbole H de focos F 1 = - c , 0 e F 2 = c , 0 e parâmetros geométricos a e b e seja r a reta tangente a H em T . Prove que, se G é o ponto simétrico de F 2 em relação a r , então G ,T e F 1 são colineares. Prove que d F 1 ,G = 2 a . Sejam G ' um ponto da circunferência de centro F 1 e raio 2 a e T ' o ponto em que a reta F 1 G ' intercepta H . Prove que G ' é o ponto simétrico de F 2 em relação à reta tangente a E em T . Conclua que o lugar geométrico dos pontos simétricos de F 2 em relação às retas tangentes à hipérbole é a circunferência de centro F 1 e raio 2 a (circunferência diretora do foco F 1 ). Por simetria, o resultado permanece válido quando permutamos F 1 e F 2 .

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 111

Seja um ponto da hipérbole de focos e e parâmetros geométricos e e seja a reta tangente a em .

Prove que, se é o ponto simétrico de em relação a , então e são colineares.

Prove que .

Sejam um ponto da circunferência de centro e raio e o ponto em que a reta intercepta . Prove que é o ponto simétrico de em relação à reta tangente a em .

Conclua que o lugar geométrico dos pontos simétricos de em relação às retas tangentes à hipérbole é a circunferência de centro e raio (circunferência diretora do foco ). Por simetria, o resultado permanece válido quando permutamos e .

Passo 1

Veja a figura abaixo:

Passo 2

Pela propriedade da reflexão, temos o ângulo que reta faz com a reta tangente é o mesmo que faz com a reta tangente (já que ). Dessa maneira, mostra-se que os pontos e são colineares.

Passo 3

Pela propriedade da elipse, temos que

Porém, como , segue que . Assim,

Passo 4

Veja a figura

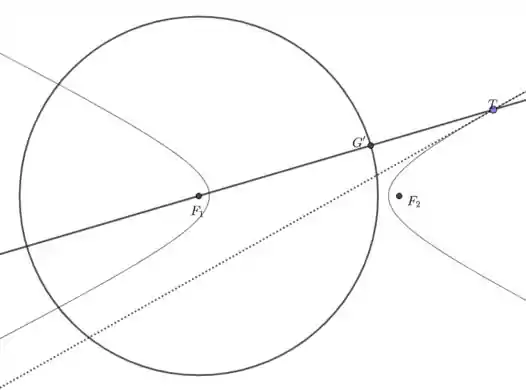
Seja a circunferência citada no enunciado. Como , então .

Da parte (a) e (b), sabemos que se é o ponto simétrico de em relação à reta tangente, então e estarão alinhados e . Porém, note na figura acima que e estão alinhados e que . Assim, só nos resta concluir que , ou seja, também é o ponto simétrico.

Passo 5

Essa é a conclusão imediata dos itens anteriores.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos casos em que a equação dada descreve uma hipérbole de focos em algum dos eixos coordenados, especifique-o e calcule a distância focal e as medidas do eixo transverso e conjugado. Faça alguns esboç

Sejam H : x 2 / a 2 - y 2 / b 2 = 1 e u → = cos ⁡ θ , sen ⁡ θ , com θ em [ 0 , π [ . Dê condições sobre θ para que(a) exista uma reta tangente a H , paralela a u → ;(b) exista uma reta normal a H para

Em cada um dos problemas 1 a 10, determinar o centro, os vértices, os focos e a excentricidade das hipérboles dadas. Esboçar o gráfico x 2 100 - y 2 64 = 1

Em cada um dos problemas 11 a 24, determinar a equação da hipérbole que satisfaz as condições dadas:Focos F ( ± 5 ,0 ) , vértices A ( ± 3 ,0 ) .

Em cada um dos problemas 11 a 24, determinar a equação da hipérbole que satisfaz as condições dadas:Focos F ( 0 ,± 3 ) , vértices A ( 0 ,± 2 ) .