Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 83
Sejam e , com em . Dê condições sobre para que
(a) exista uma reta tangente a , paralela a ;
(b) exista uma reta normal a paralela a .
Interprete geomericamente os resultados.
Passo 1
Vamos começar lembrando de algumas propriedades da parábola. A equação reduzida é essa aqui:
Onde e são números positivos.
Quando deixamos todos os parâmetros iguais a , o gráfico dela é mais ou menos assim:
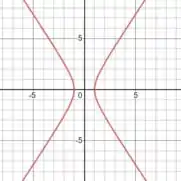
E as assíntoas da parábola são essas duas retas pontilhadas:
As equações delas são:
Outra forma de escrever isso é:
Beleza, são essas equações que dão a chave para resolver a questão!
Passo 2
(a) Nesse item a gente quer a condição para que exista alguma reta paralela a que seja tangente à parábola.
Vamos desenhar algumas dessas retas para entender o que isso quer dizer. Olhando só para o primeiro quadrante para facilitar:
Percebe que essa reta verde é um pouco mais inclinada do que a assíntota?
Para encontrar uma reta tangente à hipérbole, é só pegar a assíntota, inclinar mais um pouco e deslocar a reta até tocar na hipérbole.
Isso quer dizer que, para que uma reta possa ser tangente a , ela precisa ser mais inclinada do que a assíntota.
Mas nós vimos que a assíntota é:
Como queremos uma inclinação maior, a condição no primeiro e quarto quadrantes é:
Onde é a inclinação da nossa reta.
Essa inequação define essa região aqui:
E nos quadrantes onde o sinal é trocado a condição é:
Que define essa região aqui:
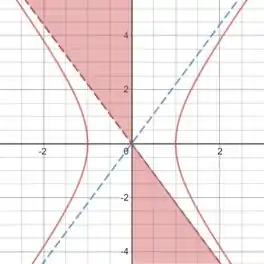
Uma forma de escrever essas duas equações de forma compacta é dizer que:
Porque quando (nos quadrantes I e III), isso vira:
E quando (nos quadrantes II e IV), isso vira:
Que é exatamente o que queremos!
Passo 3
Agora falta expressar a inclinação da nossa reta em termos do vetor , que é o vetor diretor da nossa reta:
A inclinação desse vetor é sempre a mesma:
Então a nossa condição para o item (a) é:
Então:
Passo 4
(b) Agora que já conhecemos a condição para que uma reta seja tangente à curva:
Fica mais fácil descobrir qual é a condição para que a reta seja normal a ela!
Para que uma reta seja normal à curva em um ponto, ela tem que ser normal à tangente da curva naquele ponto!
Se uma reta tangente tem esse coeficiente angular aqui:
Podemos achar o coeficiente angular da reta normal lembrando dessa relação aqui:
Substituindo isso na relação de antes:
Usando as propriedades do módulo, podemos reescrever isso como:
Então:
E a condição é>
Geometrciamente, isso quer dizer que as retas precisam estar abaixo da reta de inclinação :
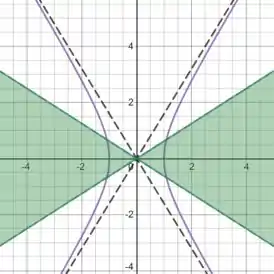
Resposta
(a) .
(b) .