Use seu programa gráfico para desenhar várias elipses no computador, com excentricidades bem espalhadas pelo intervalo . Para que a figura seja intrusiva, use para todas o mesmo valor de e exagere, dando a alguns valores muito próximos de e outros muito próximos de (não estranhe os resultados; lembre-se de que o computador não trabalha com valores exatos).

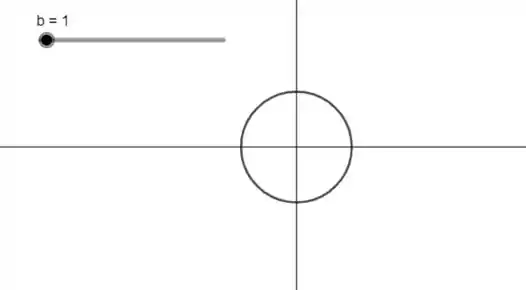
Quando , obviamente teremos uma circunferência de centro e raio .

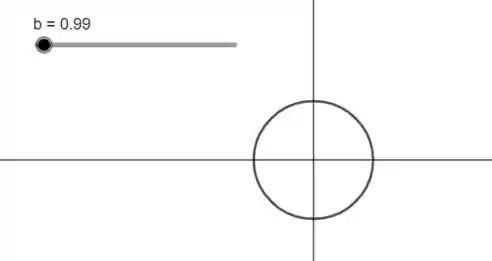
Quando é muito próximo de , a elipse irá se “confundir” com uma circunferência.

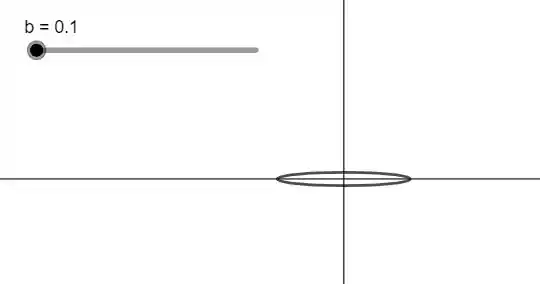
Quando se aproxima de zero, a elipse irá se degenerar para a reta .

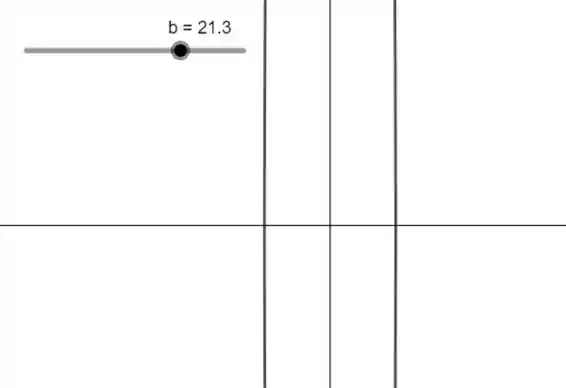
Quando é muito grande, temos esse “estranho” comportamento. Porém, note que quando é muito grande, podemos desprezar o termo . Assim, ficamos com que são as duas “retas paralelas” que vemos na imagem.