Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 25.Exercício - Ex. 08

Seja Ω a quádrica de equação 4 x 2 + y 2 + 4 z 2 - 8 x - 4 y - 8 z + 8 = 0 .

  1. Complete quadrados para provar que Ω é um elipsoide.
  2. Faça uma translação do sistema de coordenadas para eliminar os termos de primeiro grau e obter uma equação reduzida de Ω .
  3. Obtenha, em relação ao sistema antigo, equações do plano paralelo a O x y que determine elipse ou circunferência máxima no elipsoide. Faça o mesmo em relação a O x z e O y z .
  4. Faça um esboço do elipsoide e desenhe, em vista frontal, suas projeções ortogonais sobre os planos O x y , O x z e O y z .

Passo 1

  1. Temos que

    2. 4 x 2 - 2 x + y 2 - 4 y + 4 z 2 - 2 z = - 8 ⟺

    4 x 2 - 2 x + 1 + y - 2 2 + 4 z 2 - 2 z + 1 = 4 ⟺

    4 x - 1 2 + y - 2 2 + 4 z - 1 2 = 4 ⟺

    x - 1 2 + y - 2 2 4 + z - 1 2 = 1

    Passo 2

  2. Basta fazermos a translação

    3. x ' = x - 1 y ' = y - 2 z ' = z - 1

    Pois obtermos a equação

    x ' 2 + y ' 2 4 + z ' 2 = 1

    Passo 3

  • Em relação a O x y : fazendo z ' = 0 , temos:

    • x ' 2 + y ' 2 4 = 1

    No sistema original, temos z = 1 + z ' ⟹ z = 1 .

  • Em relação a O x z : fazendo y ' = 0 , temos

    • x ' 2 + z ' 2 = 1

    No sistema original, temos y = y ' + 2 ⟹ y = 2 .

  • Em relação a O y z : fazendo x ' = 0 , temos

    • y ' 2 4 + z ' 2 = 1

    No sistema original, temos x = x ' + 1 ⟹ x = 1 .

    Passo 4

  • Temos um elipsoide de centro 1 ,   2 ,   1 , conforme mostra a figura abaixo.

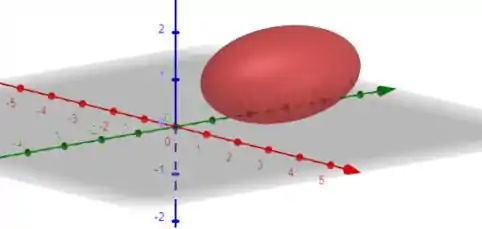
    • As projeções serão obtidas da seguinte forma:

  • No plano x y :

    • Fazendo z = 0 , temos

    x - 1 2 + y - 2 2 4 = 0

    Portanto, a projeção no plano x y é o ponto 1 ,   2,0 (o elipsoide é tangente ao plano x y ).

  • No plano x z :

    • Fazendo y = 0 , temos

    x - 1 2 + z - 1 2 = 0

    A projeção no plano x z será o ponto 1,0 ,   1 (o elipsoide é tangente ao plano x z ).

  • No plano y z :

Fazendo x = 0 , temos

y - 2 2 4 + z - 1 2 = 0

Portanto, a projeção no plano y z é o ponto 0 ,   2 ,   1 (o elipsoide é tangente ao plano y z ).

Observação: note que o gabarito está incorreto para o item (d).

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Identificar as quádricas representadas pelas equações x 2 + y 2 = 9
Identificar as quádricas representadas pelas equações 4 x 2 + 9 y 2 = 36 z
Identificar as quádricas representadas pelas equações x 2 - 4 y 2 = 16
Identificar as quádricas representadas pelas equações 16 x 2 + 9 y 2 - z 2 = 144
Identificar as quádricas representadas pelas equações z 2 = x 2 + y 2