Enunciado
Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 4.Exercícios Propostos - Ex. 21
Sejam .
- Calcule a área do triângulo ABC.
- Determine um vetor , de módulo 1, perpendicular ao plano ABC. Desenhe um representante de
- Desenha na figura ao lado um representante de
Passo 1
E aí pessoal, beleza?
Para o item a) basta calcularmos:
Como:
Passo 2
Agora vamos calcular o produtor vetorial:
Passo 3
Passo 4
Para o item b, como pede um vetor de módulo 1, basta dividirmos o vetor pelo módulo:
Passo 5
Agora para o item c), só precisamos desenhar um vetor perpendicular ao plano:
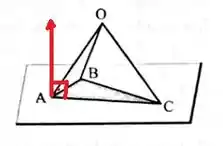
Fechou! Vamos pra próxima?
Resposta
Exercícios de Livros Relacionados
Dados os vetores u → = 2 ,1 ,0 e v → = ( 3 , - 6 ,9 ) , determinar o vetor x → que satisfaz a relação v → = u → × x → e que seja ortogonal ao vetor w → = ( 1 , - 2 ,3 ) .
Dado o triângulo de vértices A 0 ,1 , - 1 , B ( - 2 ,0 ,1 ) e C ( 1 , - 2 ,0 ) , calcular a medida da altura relativa ao lado B C .
Sejam u , v e w vetores não nulos com o mesmo ponto inicial no espaço tridimensional, mas tais que dois quaisquer não são colineares. Mostre que u × v × w está no plano determinado por u e v
Determine o produto vetorial a × b e verifique que ele é ortogonal a a e b .
Efetuare) (3 vec i) . ( 2 vec j )