Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 5.Exercícios Propostos - Ex. 6

Sejam A B →   =   ( 3,6 , 3 )   , A C →   =   ( 1,3 , - 2 )   e A D →   = ( 2,2 , α - 2 ) . Encontre os valores do parâmetro α para os quais o volume V do tetraedro A B C D fica igual a 3 .

Passo 1

Tudo bem, gente? Não sei se vocês lembram, mas o volume do tetraedro é dado por

V = 1 6 | [ A B , → A C → , A D → ] |

Então, vamos calcular esse produto misto, substituir na fórmula do volume e igualar a 3. Prontos ou não, aí vamos nós:

[ A B , → A C → , A D → ] = 3 [ 3 α - 6 + 4 ] - 6 [ α + 2 ] + 3 ( - 4 ) = 9 α + 3 ( - 2 ) - 6 α - 12 - 12

[ A B , → A C → , A D → ] = 3 α - 6 - 12 - 12 = 3 α - 30 = 3 ( α - 10 )

⇒ V = 1 6 | [ A B , → A C → , A D → ] | = | 3 ( α - 10 ) 6 | = | ( α - 10 ) | 2

V = 3 ⇒ | ( α - 10 ) | 2 = 3 ⇒ | α - 10 | = 6

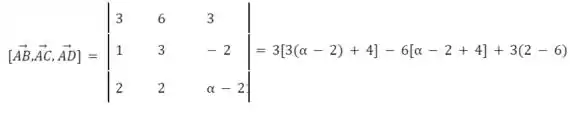
Com isso, vemos que existem dois valores possíveis de α que satisfazem | α - 10 | = 6 : α = 16 e α = 4 .

Resposta

α = 16 e α = 4

Exercícios de Livros Relacionados

Sendo |vec u| = 3 , |vec v| = 4 e 120 ° o ângulo entre os vetores vec u e vec v , calcular:b) |vec u xx (vec v - vec u)|
Três vértices de um tetraedro de volume 6 são A - 2,4 , - 1 ,B - 3,2 , 3 eC 1 , - 2 - 1 . Determinar o quarto vértice D , sabendo que ele pertence ao eixo O y .
Sabendo que os vetores A B → = 2,1 , - 4 ,A C → = m , - 1,3 eA D → = ( - 3,1 - 2 ) determinam um tetraedro de volume 3 , calcular o valor de m .
Calcular a distância do ponto D ( 2,5 , 2 ) ao plano determinado pelos pontos A 3,0 , 0 ,B 0 , - 3,0eC ( 0,0 , 3 ) .
Representar graficamente o tetraedro ABCD e calcular seu volume, sendo A 1,1 , 0 ,B 6,4 , 1 ,C 2,5 , 0e D ( 0,3 , 3 ) .