Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 4.Problemas propostos - Ex. 14
Representar graficamente o tetraedro ABCD e calcular seu volume, sendo .
Passo 1
E aí, tudo joia?
O volume do tetraedro é do volume do paralelepípedo, ou seja:
Vamos fazer o produto misto então e dividir por 6😊
Mas primeiro...
Vamos ver o tetraedo:
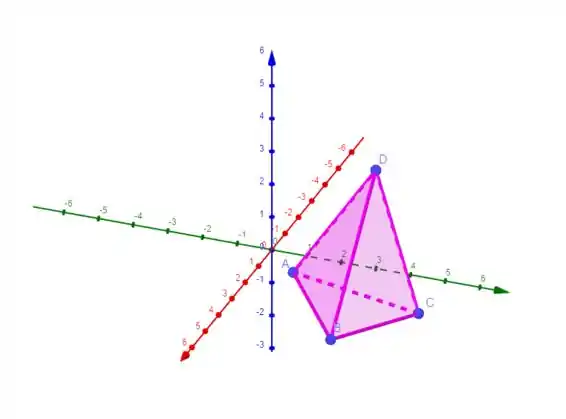
Passo 2
Depois de ver essa lindeza dá até uma animada né?
Bora calcular os vetores então...
Passo 3
Agora a gente vai fazer o produto misto...
O produto misto é dado pelo determinante da matriz formada pelos vetores:
O volume do tetraedro então é:
Prontinho😉
Resposta
Exercícios de Livros Relacionados
69. Para que valor de m os pontos A m , 1,2 ,B 2 - 2 , - 3 ,C 5 , - 1,1 e D 3 , - 2 , - 2 são coplanares?
75. Calcular o volume do tetraedro A B C D , sendo dados:a) A 1,0 , 0 , B 0,1 , 0 , C 0,0 , 1 e D 4,2 , 7 b) A - 1,3 , 2 , B 0,1 , - 1 , C - 2,0 , 1 e D 1 , - 2,0 . Para este, calcular também a medida
75. Calcular o volume do tetraedro A B C D , sendo dados:a) A 1,0 , 0 , B 0,1 , 0 , C 0,0 , 1 e D 4,2 , 7 b) A - 1,3 , 2 , B 0,1 , - 1 , C - 2,0 , 1 e D 1 , - 2,0 . Para este, calcular também a medida
70. Determinar o valor de k para que os seguintes vetores sejam coplanares:a) a = 2 , - 1 , k ,b = 1,0 , 2 e c = k , 3 , k b) a = 2,1 , 0 ,b = 1,1 , - 3 e c = k , 1 , - k c) a = 2 , k , 1 ,b = 1,2 , k
73. Os vetores a = 2 , - 1 , - 3 ,b = - 1,1 , - 4 e c = m + 1 , m , - 1 determinam um paralelepípedo de volume 42. Calcular m .