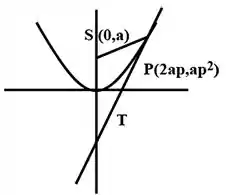
Sejam P um ponto da parábola y=a x ² ² e P ’ o ponto em que a tangente a essa parábola pelo ponto P corta o eixo 0 Y . Mostre que P e P ' são equidistantes do eixo 0 X . A partir daí, obtenha um método gráfico para traçar a tangente por P.

d =0 - 0 2 + a - a p 2 2 = | a + a p 2 | d 1 =2 a p - 0 2 + a - a p 2 2 d 1 = a 2 + a ² p 4 + 2 a ² p ² ² ² ² d 1 = a 2 + a ² p 4 + 2 a ² p ²= | a + a p 2 | ² ² ² Ou seja temos d = d 1 provando assim que ambos os pontos são equidistantes.Graficamente:

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 18.Problemas - Ex. 8

Sejam P um ponto da parábola e o ponto em que a tangente a essa parábola pelo ponto P corta o eixo . Mostre que e são equidistantes do eixo . A partir daí, obtenha um método gráfico para traçar a tangente por P.

Passo 1

Olá galera! tudo bem?

Bora junto resolver mais um problema!

Esse é exercício é totalmente algébrico pois se trata de uma demonstração. Beleza!

Preparado?

Inicialmente sabemos que a equação da parábola terá a equação e dois pontos o que pertence, vou chama-lo de a parábola e P’ que pertence a uma reta tangente a parábola vou chama-lo apenas de

Vamos começar então!

Para a reta tangente teremos que:

Para a reta tangente no eixo y temos:

Utilizando o conceito de geometria analítica de distância de pois pontos, vamos obter:

Ou seja temos provando assim que ambos os pontos são equidistantes.

Graficamente vamos obter:

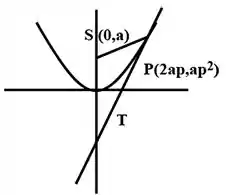
Prontinho, acabamos te vejo na próxima questão!

Resposta

Ou seja temos provando assim que ambos os pontos são equidistantes.

Graficamente:

Exercícios de Livros Relacionados

5.1. 4. Escreva as equações das seguintes parábolas: (a) O foco é F = (0, 2) e diretriz y = −2;

Mostre que a equação da parábola com foco no ponto F = ( x 0 + p , y 0 ) e a reta diretriz r : x = x 0 - p é y - y 0 2 = 4 p ( x - x 0 ) .

Mostre que um espelho parabólico reflete na direção do foco os raios que incidem paralelos ao seu eixo de simetria seguindo os seguintes passos:

Identificar a cônica, achar a equação no último sistema de coordenadas utilizando e fazer um esboço do gráfico. 8 x 2 + 8 y 2 - 16 x y + 33 2 x - 31 2 y + 70 = 0