Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 2.Exercícios Propostos - Ex. 8

Sejam O, A, B e C quatro pontos tais que O A     → =   a →   +   b → , e O B   → =   3 a →   -   2 b → e O C   → =   2 a →   + m b → . Sendo a →   e b → vetores l.i., determine m para que os vetores A C   → e B C   → sejam l.d.. Ilustre o problema com um desenho.

Passo 1

Galera, lembrando do conceito de dependência linear, temos que A C   → e B C   → são l.d. se A C   → = α B C → . Tá, mas como definir A C   → e B C   → ? É simples, é só usar os vetores que já conhecemos O A     → =   a →   +   b → , e O B   → =   3 a →   -   2 b → e O C   → =   2 a →   + m b → :

A C   → = A O   → + O C   → = - O A   → + O C   → = - ( a →   +   b → ) + 2 a →   + m b → = a →   + ( m - 1 ) b →

B C   → = B O   → + O C   → = - O B   → + O C   → = - ( 3 a →   -   2 b → ) + 2 a →   + m b → = - a →   + ( m + 2 ) b →

Passo 2

Agora, nós substituímos

A C   → = a →   + ( m - 1 ) b →

B C   → = - a →   + ( m + 2 ) b →

em A C   → = α B C → :

a →   + ( m - 1 ) b → = α ( - a →   + ( m + 2 ) b → ) = - α a →   + ( m + 2 ) α b →

⇒ ( 1 + α ) a →   = [ ( m + 2 ) α - m + 1 ] b →

Como a →   e b → são vetores l.i., então a equação acima só é verdadeira se ambos os lados forem nulos, ou seja,

1 + α = 0 ⇒ α = - 1

( m + 2 ) α - m + 1 = 0 ⇒ - m - 2 - m + 1 = - 2 m - 1 = 0 ⇒ m = - 1 2 .

Passo 3

Para fechar com chave de ouro, um desenho mostrando o que acabamos de fazer:

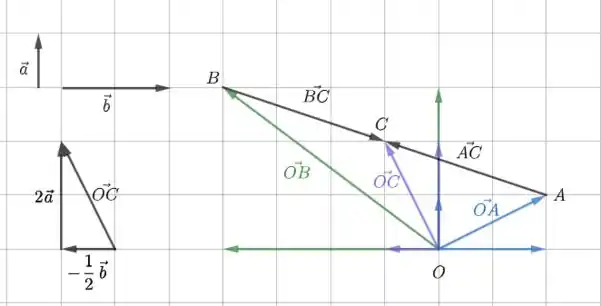
Aqui, fica bem claro todos os vetores envolvidos e que A C   → e B C   → são l.d.

Resposta

m = - 1 2

Exercícios de Livros Relacionados

Exprima o vetor w = (1, 1) como combinação linear de u = (−2, 1) e v = (1, −1).
Se os vetores u ,vew não são coplanares, mostre geometricamente que todo vetor do espaço se exprime como combinação linear
Dados quatro vetores no espaço, prove que um deles é combinação linear dos outros três.
Determine quais dos seguintes conjuntos é tal que nenhum dos seus vetores é combinação linear dos outros dois: a ){ ( 1 ,- 1 ,2 ) , ( 1 ,1 ,0 ) , ( 1 ,- 1 ,1 ) } b ){ ( 2 ,1 ,2 ) , ( 1 ,- 1 ,1 ) , ( 5
Sejam r 1={ A+s·v ;s∈R }er 2={ B+t·w ;t∈R } duas retas:i) Prove que r 1=r 2 se, e somente se, os vetores A B → e w são múltiplos de v .ii) Prove que r 1er 2 são coplanares se, e somente se, os vetores