Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 28.Problemas - Ex. 11

Determine quais dos seguintes conjuntos é tal que nenhum dos seus vetores é combinação linear dos outros dois:

a )   { ( 1 ,   - 1 ,   2 ) , ( 1 ,   1 ,   0 ) , ( 1 ,   - 1 ,   1 ) }  

b )   { ( 2 ,   1 ,   2 ) , ( 1 ,   - 1 ,   1 ) , ( 5 ,   4 ,   2 ) }  

c )   { ( 1 ,   0 ,   - 2 ) , ( 2 ,   - 1 ,   2 ) , ( 4 ,   - 3 ,   10 ) }  

d )   { ( 1 ,   - 1 ,   1 ) , ( - 1 ,   2 ,   1 ) , ( - 1 ,   2 ,   2 ) } .

Passo 1

Saudações galerinha, tudo bem?

Vamos começar a resolver mais um exercício, bora lá então!

Inicialmente temos um problema longo mais não desiste!

Para resolver esse problema vamos entende um pouco da combinação linear em três dimensões, os vetores formam um paralelogramos, se esse paralelogramo tiver um volume significa que os vetores são combinação linear.

Mas como encontrar esse volume?

Simples basta encontrar o determinante formado pelos vetores, se for um número real os vetores formam uma combinação linear senão os vetores não serão combinação linear entre eles.

Começaremos testando

Formando o determinante e já calculando o mesmo entre   { ( 1 ,   - 1 ,   2 ) , ( 1 ,   1 ,   0 ) , ( 1 ,   - 1 ,   1 ) }   , teremos:

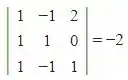
Neste caso temos o determinante negativo, não existe volume negativo logo esse vetores não são combinação linear entre si.

Passo 2

Formando o determinante e já calculando o mesmo entre     { ( 2 ,   1 ,   2 ) , ( 1 ,   - 1 ,   1 ) , ( 5 ,   4 ,   2 ) }     , teremos:

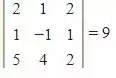
Neste caso temos o determinante positivo, logo esse vetores são combinação linear entre si.

Até aí tranquilo?

Passo 3

Formando o determinante e já calculando o mesmo entre { ( 1 ,   0 ,   - 2 ) , ( 2 ,   - 1 ,   2 ) , ( 4 ,   - 3 ,   10 ) }     , teremos:

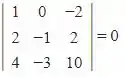
Neste caso temos o determinante nulo , não existe volume nulo logo esse vetores não são combinação linear entre si.

Passo 4

Quase acabando!

Formando o determinante e já calculando o mesmo entre { ( 1 ,   - 1 ,   1 ) , ( - 1 ,   2 ,   1 ) , ( - 1 ,   2 ,   2 ) } .   , teremos:

Neste caso temos o determinante positivo, logo esse vetores são combinação linear entre si.

Prontinho!

Acabamos te vejo na próxima questão!

Resposta

Os vetores     { ( 2 ,   1 ,   2 ) , ( 1 ,   - 1 ,   1 ) , ( 5 ,   4 ,   2 ) }     e { ( 1 ,   - 1 ,   1 ) , ( - 1 ,   2 ,   1 ) , ( - 1 ,   2 ,   2 ) } são combinação linear entre si.

Exercícios de Livros Relacionados

A sequência ( u → ,v → ,w → ) é LD. Verifique se são verdadeiras ou falsas as afirmações seguintes (justifique sua resposta).a) Necessariamente, um dos vetores é nulo.b) Se u → ≠ 0 , então v → | | w →
Sejam u → = P A → ,v → = P B → ,w → = P C → . Prove:a) P ,A ,B e C são coplanares ⇔ ( u → , v → ,w → ) é LD.b) P ,A e B são colineares ⇔ ( u → ,v → ) é LD.
Prove que, se u → é um múltiplo escalar de v → ( u → = λ v → ), então qualquer sequência que contém u → e v → é LD. Em particular, toda sequência de vetores que contém o vetor nulo é LD.
Prove:a) ( vec u , vec v , vec w ) é LI = ( vec u + vec v , vec u + vec w , vec v + vec w ) é LI.b) ( vec u , vec v , vec w ) é LI = ( vec u + vec v + vec w , vec u - vec v , 3 vec v ) é LI.
Para garantir, na demonstração da Proposição 6-8, que os pontos M ,N ,Q e R são univocamente determinados, explique por quê:a) a reta paralela a P C por D não é paralela ao plano P A B .b) a reta para