Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 3.Exercício - Ex. 16
16.. Sendo o ponto médio de , o de BD e, prove que
Passo 1
Vamos tentar reescrever a soma .
E tentar tentar reescrever a soma .
Passo 2
Vamos nos focar na primeira soma e no primeiro fator dessa soma, o ,
pode ser escrito assim:
E o também pode ser escrito assim:
Somando esses dois, temos:
Olha a figura:
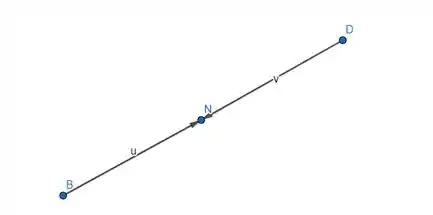
Repare bem na figura e você vai perceber isso:
Então
Passo 3
Agora vamos focar na soma .
Faremos exatamente do mesmo jeito
E o :
Somando essas duas temos:
Pelo que vimos no passo 3 a soma , então:
Agora colocando as duas expressões e somando!
O vetor pode ser escrito dessas duas formas:
Somando as duas temos:
Só que vamos desenhar os vetores para você visualizar algo bacana!
A soma , já que esses vetores são opostos!
Então,
Substituindo essa expressão em , temos:
O que demostra que é paralelo a .
Resposta
Ei, a resposta está no passo a passo :)