Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 2.Problemas Propostos - Ex. 31c
31. Seja o cubo de aresta representado na Figura 2.17.
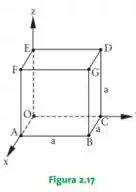
Determinar:
c)
Passo 1
Então galera, de acordo com o que estudamos no capítulo em questão do Winterle, temos que o produto escalar entre dois vetores é dado da seguinte forma:
No qual é o ângulo entre os dois vetores. Queremos determinar , certo? No desenho, os vetores seriam esses aqui em azul ó:
Note que o ângulo entre os vetores é de , pois os vetores estão em planos DISTINTOS! Logo:
E como , então:
E essa é a nossa resposta, galera! 😉
Resposta
Exercícios de Livros Relacionados
Sabendo que u → = 2 ,v → = 3 e que u → ev → formam um ângulo de 3 π 4 r a d , determinar: u → - 2 v →
Qual deve ser o valor de α para que os vetores a → = α i + 2 j - 4 k e b → = 2 i + 1 - 2 α j + 3 k sejam ortogonais?
Sabendo que u → = 2 ,v → = 3 e u → . v → = - 1 , calcular: 3 u → + 4 v → . ( - 2 u → - 5 v → )
Verificar para os vetores u → = 4 , - 1,2 e v → = ( - 3,2 , - 2 ) as desigualdades: u → + v → ≤ u → + v →( D e s i g u a l d a d eT r i a n g u l a r )
Verificar para os vetores u → = 4 , - 1,2 e v → = ( - 3,2 , - 2 ) as desigualdades: u → . v → ≤ u → v →( D e s i g u a l d a d ed eS c h w a r z )