Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 2.Exercício - Ex. 6
6. Você dispõe de uma folha de papel circular, de centro O. Verifique se existem pontos na borda da folha tais que não seja possível desenhar os representantes e (entenda desenhar representante como desenhar a flecha correspondente).
Passo 1
Vamos entender o que ele quer nessa questão! Ele quer que a gente pegue dois pontos na borda da folha e que desenhamos os vetores.
Temos que desenhar dois pontos em que a soma não está na borda e nem a diferença!!
Passo 2
Vamos começar desenhando alguns pontos!
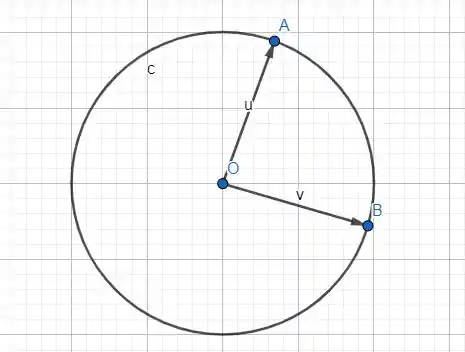
Se fizermos a soma desses vetores, de acordo com a regra do polígono, teríamos algo assim:
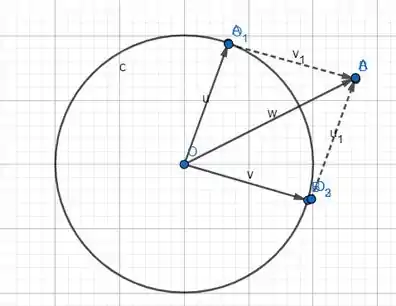
Ou seja, não conseguiríamos desenhar a soma, vamos tentar agora a diferença!
Passo 3
A diferença é a outra diagonal do parelologramo!
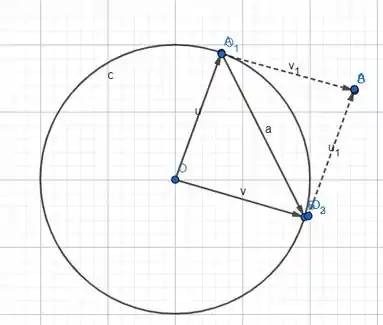
Essa nós já conseguimos desenhar, ou seja, sempre conseguiremos desenhar pelo menos um representante! O que demonstra que se temos essa folha do enunciado, não tem jeito!!! Um representante a gente consegue!
Resposta
Ei, a resposta está no passo a passo :)