Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 3.Exercício - Ex. 17
17.Sejam ABCD um quadrilátero, ponto qualquer e o ponto médio que une os pontos médios da diagonais e .Prove que
Passo 1
Vamos reescrever todos os vetores:
Passo 2
Vamos começar reescrevendo
Vamos reescrever , da mesma forma que .
Vamos reescrever , da mesma forma que .
Vamos reescrever , da mesma forma que .
Agora vamos somar todos esses vetores.
Passo 3
Paramos nessa expressão.
Vamos desenhar esse quadrilátero com as diagonais.
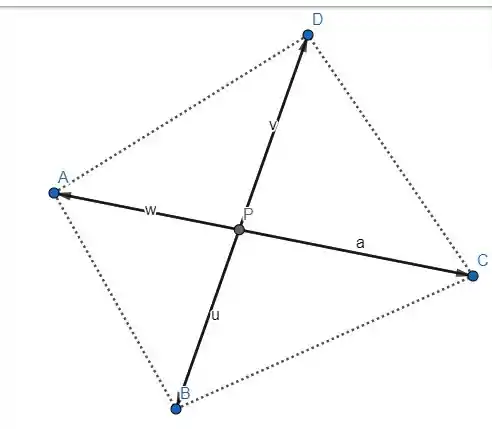
O ponto é o ponto médio.
, já que esses vetores são opostos.
, já que esses vetores são opostos.
Então:
Prontoo! Demonstramos aquilo do enunciado.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
22. Seja o vetor v → = 2 ,- 1 ,1 . Obter:b) Um vetor unitário ortogonal a v → ;
Sejam u → = m , - 1 , m 2 + 1 , v → = ( m 2 + 1 , m , 0 ) e w → = m , 1,1 . Mostre que C = ( u → , v → , w → ) é uma base de V , independentemente do valor de m .
Seja E = e → 1 , e → 2 , e → 3 uma base . Sejam f 1 → = e → 1 - e → 2 + e → 3 , f 2 → = e → 2 + e → 3 e f 3 → = - 2 e → 3 (a)Mostre que F = ( f 1 → , f 2 , → f 3 → ) também é uma base.
Dados os pontos A - 1 ,0 ,5 , B 2 ,- 1 ,4 e C 1 ,1 ,1 , determinar x tal que A C → e B P → sejam ortogonais, sendo P x ,0 ,x - 3 .
Dados os vetores a → = 2 ,1 ,α , b → = α + 2 ,- 5 ,2 e c → = 2 α ,8 ,α , determinar o valor de α para que o vetor a → + b → seja ortogonal ao vetor c → - a → .