Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.12 - Ex. 18
Os traços físicos são determinados pelos genes que um descendente recebe de seus dois ascendentes. No caso mais simples, um traço no descendente é determinado por um par de genes, um de cada um dos dois ascendentes. Em geral, cada gene num par pode tomar uma de duas formas, denotadas por e , que são os alelos. Isso leva a três pareamentos possíveis, a saber,
Denominados genótipos (os pares determinam o mesmo traço e são, portanto, indistinguíveis). Mostra-se no estudo da hereditariedade, que se um dos ascendentes tiver genótipo conhecido e o outro ascendente for de genótipo aleatório, então o descendente terá a probabilidade de genótipo dada na próxima tabela, que pode ser vista como uma matriz de transição de um processo de Markov.
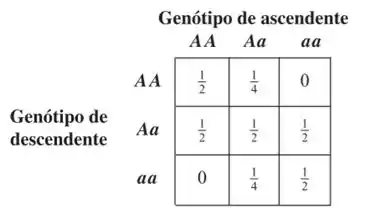
Assim, por exemplo, o descendente de um ascendente de genótipo e de outro escolhido aleatoriamente e de genótipo desconhecido tem uma chance de de ser , de ser e nenhuma chance de ser .
Mostre que a matriz de transição é regular.
Encontre o vetor estacionário e discuta sua interpretação física.
Passo 1
Primeiramente temos que nossa matriz de transição vai ser dada por
Podemos dizer que a matriz acima é estocástica, pois a soma das entradas em cada coluna é 1 e duas entradas da matriz são 0. Tomemos então, nossa matriz de transição e façamos
Como, todas as entradas de são não negativas temos que a matriz é uma matriz regular.
Passo 2
Agora, tomemos como nosso vetor de estado estacionário onde (onde é uma matriz de dimensão ). Assim, teremos
Além disso, devemos ter que
Então,
A partir daí temos o seguinte sistema de equações
Como devemos ter que a soma dos valores de deve ser igual a vamos ter
Dessa forma podemos concluir que
Assim, nosso vetor de estado estacionário será
Resposta