Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 16

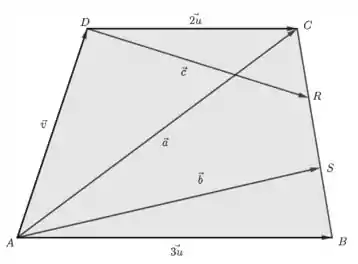
No trapézio ABCD ao lado, temos A B → = 3 u → , C D → = 2 u → , A D → = v → , A C → = a → , A S → = b → e D R → = c → . Sendo R e S os pontos de trissecção do lado BC,

  1. Escreva a → , b → e c → em função de u → e v → .
  2. Escreva c → em função de a → e b → .

Passo 1

  1. O truque para resolver essa questão é notar que B S → = R C → = 1 3 B C → porque R e S são os pontos de trissecção de BC, ou seja, eles dividem BC em três partes iguais. Além disso, temos

    2. B C → = B A → + A D → + D C → = - 3 u → + v → + 2 u → = v → - u →

    Sabendo disso, podemos usar os conceitos de soma de vetores para obter os vetores pedidos na questão:

    a → = A C → = A D → + D C → = v → + 2 u →

    b → = A S → = A B → + B S → = A B → + 1 3 B C → = 3 u → + 1 3 ( v → - u ) → = 8 3 u → + 1 3 v →

    c → = D R → = D C → + C R → = D C → - R C → = D C → - 1 3 B C → = 2 u → - 1 3 ( v → - u ) → = 7 3 u → - 1 3 v →

    Passo 2

  2. Para escrever c → em função de a → e b → , vamos assumir que c → = x a → + y b → e comparar ambos os lados das equações. Com isso, vamos obter um sistema de equações para x e y e a solução desse sistema nos dará a combinação linear que queremos. Assim,

c → = 7 3 u → - 1 3 v → = x a → + y b → = x ( v → + 2 u → ) + y ( 8 3 u → + 1 3 v → ) = u → ( 2 x + 8 3 y )   +   v → ( x + 1 3 y )

⇒ 2 x + 8 3 y = 7 3

x + 1 3 y = - 1 3

Vamos multiplicar ambos os lados das duas equações por três:

6 x + 8 y = 7

3 x + y = - 1

Vamos multiplicar a segunda equação por dois e subtrair da primeira. Com isso, obtemos

6 x + 8 y - 2 ( 3 x + y ) = 6 x + 8 y - 6 x - 2 y ) = 6 y = 7 - 2 ( - 1 ) = 9 ⇒ y = 9 6 = 3 2

Substituindo esse resultado na segunda equação, obtemos

3 x + 3 2 = - 1 ⇒ 3 x = - 1 - 3 2 = - 5 2 ⇒ x = - 5 6

Logo, devemos ter

c → = x a → + y b → = - 5 6 a → + 3 2 b →

Resposta

  1. a → = v → + 2 u → , b → = 8 3 u → + 1 3 v → , c → = 7 3 u → - 1 3 v →
  2. c → = - 5 6 a → + 3 2 b →

Exercícios de Livros Relacionados

O A →=( 4 , - 3 , - 1 ) , O B →=( - 5,3 , - 7 ) e O C →=( 1 , y , z ) . Determine y e z sabendo que C pertence à reta AB.
Dados os vetores u →=( 1 , - 1,3 ) , v →=( 2,0 , 1 ) e w →=( 3,1 , - 1 ) , determine um vetor x → paralelo a v → e tal que u→ + x → seja paralelo a w → .
No Δ A B C temos A B→ =b → , A C→ =c → , 3 A P→ =2 P C → e B Q→ = λB C → . Determine λ → para que P Q → fique paralelo ao vetor 2 A B→ +A C →+B C → .
Sejam a→ e b→ não paralelos, O A→ =a →- 2b → , O B→ = 2a →- b → e O C→ = ta →+b → . Determine t de modo que tenhamos A C→ / /B C → . Desenhe todos os vetores.
Sendo 3 vec A B + 2 vec B C = vec 0 , prove que vec O A , vec O B e vec O C são l.d. para qualquer O .