Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 3.Exercícios Propostos - Ex. 5

Sejam , e .

Calcule o comprimento dos lados do triângulo ABC.

Calcule o coseno do maior ângulo do triângulo ABC.

O triângulo ABC é acutângulo? Explique sua resposta.

Passo 1

Fala, gente boa! Antes de mais nada, vamos usar as informações do enunciado e desenhar o triângulo:

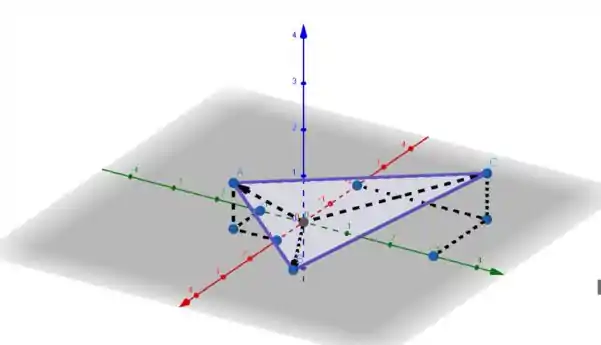
Para o item a), precisamos notar que A, B e C são os vértices do triângulo. Então, para obter o comprimento dos lados do triângulo, temos que descobrir o módulo dos vetores , e já que essas são as arestas do triângulo. Assim,

Agora que conhecemos os vetores, podemos calcular seus módulos:

Passo 2

Como temos a relação

só precisamos identificar qual é o maior ângulo. Na figura do Passo 1, vemos que é o ângulo do vértice B, que chamaremos de . Assim,

Resposta

, e

Exercícios de Livros Relacionados

Determine os vetores unitários u → = x , y ,z B tais que a projeção ortogonal de u → sobre k → seja k → / 2 e a medida angular entre v → = x ,y ,0 B e i → seja π / 6 radianos.

Prove que, se lambda != 0 e vec u != vec 0 , então p r o j_vec u vec v = p r o j_lambda vec u vec v .

a) Mostre que, se u → é unitário, então p r o j u →v → = v → ⋅ u → u → .b) Seja B = ( i → ,j → ,k → ) uma base ortonormal. Mostre que todo vetor u → é a soma de suas projeções ortogonais sobre i → , j

Prove que as bissetrizes de ângulos adjacentes suplementares são perpendiculares.

a) No exercício resolvido anterior, suponha que u → , v → e w → sejam não-nulos, não necessariamente unitários. Pode-se ainda concluir que ( u → ,v → ,w → ) é base?c) Mostre que, se u → , v → e w → sã