Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 27

Demonstre: Em um quadrilátero qualquer ABCD, os pontos médios M, N, P e Q dos lados são vértices de um paralelogramo.

Passo 1

Essa é uma daquelas questões que é tão óbvia visualmente que às vezes a gente acha que nem precisa de demonstração. Veja, por exemplo, a figura abaixo:

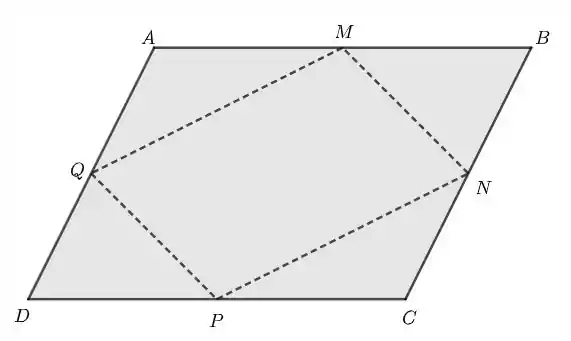
Ok! Está bem claro que os pontos médios são vértices de um paralelogramo. Mas como provar isso? Bom, num paralelogramo os lados opostos são paralelos e de mesmo comprimento. É isso que devemos mostrar.

Passo 2

Vamos começar verificando que Q P → = M N → . Vamos escrever esses dois vetores em termos de A B → e A D → e verificar que obtemos o mesmo resultado. Como ABCD é um paralelogramo, então A B → = D C → e A D → = B C → . Além disso, para os pontos médios vale A M → = 1 2 A B → , B N → = 1 2 B C → e assim por diante. Com essas informações, podemos calcular:

Q P → = Q D → + D P → = 1 2 A D → + 1 2 D C → = 1 2 A D → + 1 2 A B →

M N → = M B → + B N → = 1 2 A B → + 1 2 B C → = 1 2 A B → + 1 2 A D →

Assim, conseguimos mostrar que Q P → = M N → .

Passo 3

Agora vamos verificar que Q M → = P N → . Temos

Q M → = Q A → + A M → = - A Q → + A M → = - 1 2 A D → + 1 2 A B →

P N → = P C → + C N → = P C → - N C → = 1 2 D C → - 1 2 B C → = 1 2 A B → - 1 2 A D →

Então, como os lados opostos de MNQP são paralelos e de mesmo comprimentos, concluímos que a figura se trata de um paralelogramo.

Resposta

Ver a resolução acima.

Exercícios de Livros Relacionados

Verdadeiro ou falso. Explique. A B →+B C →=A C → implica que A, B e C são colineares.Se os 4 pontos A, B, C, e D são não coplanares, então os vetores A B → e C D → também são não coplanares.Na figura,
Se possível, desenhe. Se impossível, explique por que. ( u → ,v → ) l.d., ( v → ,w → ) l.i. e ( u → ,v → ,w → ) l.d.; ( u → ,v → ) l.d., ( v → ,w → ) l.i. e ( u → ,v → ,w → ) l.i.; ( u → ,v → ) l.d.,
No hexágono A B C D E F temos A B→ = 2a → , F C→ = 7a → , E D→ =3 a → e B C→ = F E →=b → . Expresse v →=C S → como combinação linear de a → e b → , sabendo que A S→ / /B C → .
Sejam O, A, B e C quatro pontos tais que O A → =a →+b → , e O B→ =3 a →-2 b → e O C→ =2 a →+ m b → . Sendo a → e b → vetores l.i., determine m para que os vetores A C→ e B C→ sejam l.d.. Ilustre o pro
Quais dos seguintes conjuntos de vetores são linearmente dependentes? { 1,1 , 1,1 , 2,3 , 1,2 , 3,1 , 2,1 , ( 2,2 , 1,1 ) }