1. Antes de mais nada, vamos desenhar um hexágono regular e os vetores , ,, , :



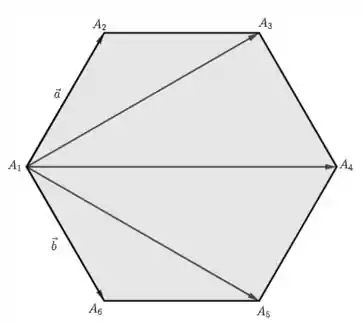
O enunciado já nos deu e , então só precisamos obter os outros três vetores. Um hexágono regular tem os seus seis lados de tamanhos iguais e pode ser dividido em seis triângulos equiláteros que se encontram no centro O como na figura abaixo:



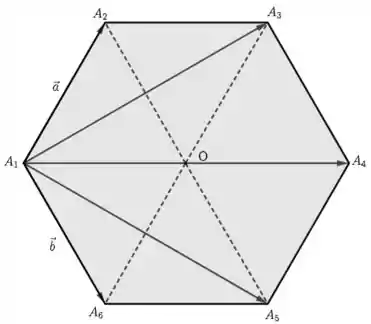
Mas espera um pouco. Como todos os lados do hexágono são iguais e os triângulos são equiláteros (todos os lados iguais), então . Da mesma forma, e temos o seguinte paralelogramo:



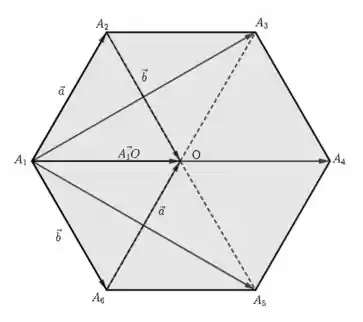
A partir dessa figura fica bem claro que

Mas se você prestar bem atenção, o vetor é exatamente o dobro do vetor . Então,

Outro detalhe muito importante a se notar é que porque eles têm o mesmo módulo, direção e sentido. Perfeito! Agora podemos encontrar os dois vetores que faltam. Olhando para a figura acima, podemos ver que

Passo 2

2. O item b pede que a gente mostre que . Então, temos que somar todos os vetores obtidos no passo anterior e ver que o resultado é seis vezes , que também foi obtido no passo anterior. Então, temos

Passo 3

3. Agora, temos que escrever em função de e . Nós vamos fazer o seguinte: vamos dizer que então vamos comparar ambos os lados da equação para obter e . Assim,

Então temos que resolver o sistema

Subtraindo a segunda equação da primeira, obtemos . Agora, substituímos esse resultado em qualquer uma das duas equações e encontramos . Logo,