Verdadeiro ou falso. Explique.
- implica que A, B e C são colineares.
- Se os 4 pontos A, B, C, e D são não coplanares, então os vetores e também são não coplanares.
- Na figura, . Os vetores , e são coplanares.
Passo 1
- Vamos começar relembrando a definição de pontos colineares. Pontos colineares são pontos que pertencem a uma mesma reta. Nesse item, temos uma reta que vai de A a C, mas não necessariamente passa pelo ponto B. Na figura abaixo, temos um exemplo onde isso ocorre.
- Como os pontos A,B,C e D não são coplanares, quer dizer que, pelo menos um dos pontos, não está no plano que contém os demais. Na figura abaixo, somente o ponto A não pertence ao mesmo plano que B,C e D, o que significa que os quatro pontos são não coplanares.
- A figura em questão é a seguinte:
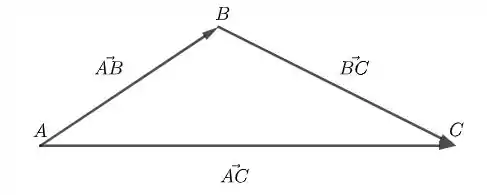
Assim, A,B e C não são colineares. Falso
Passo 2

Agora vamos desenhar os vetores e .
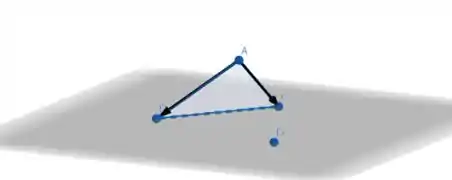
Nesse caso, conseguimos ver claramente que e estão num mesmo plano. Logo, a afirmação é falsa.
Passo 3
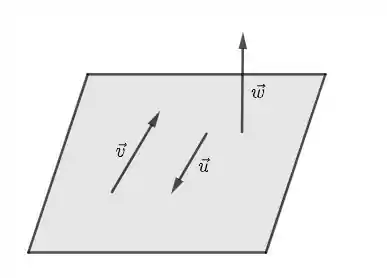
Embora não pareça, , e estão contidos num mesmo plano. Veja só a figura seguinte:
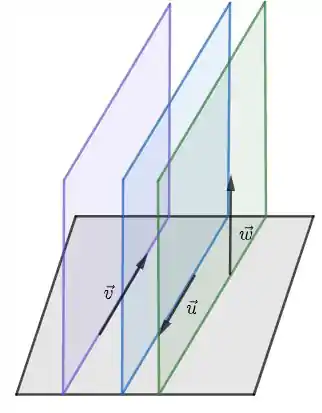
Vemos que existem vários planos paralelos que contém , e , logo eles são coplanares e a afirmação é verdadeira.
Resposta
- Falsa
- Falsa
- Verdadeira