Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 6.Exercício - Ex. 16.b
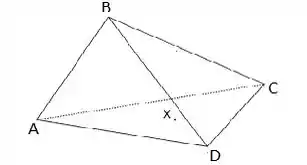
16 No tetraedro ABCD, sejam M, N e P, respectivamente, os pontos médios de BD, CD, e AC, e G o baricentro do triângulo MNP.
- Exprima como combinação linear de
- Calcule m para que o ponto pertença ao plano da face ACD.
Passo 1
Opaa... vamos lá???
Nessa questão vamos precisar da resposta da letra a:
E pra o ponto pertencer ao plano , vamos ter que dizer que são linearmente dependentes.
Passo 2
Pra gente importa que sejam LD a gente usa a equação:
E que essa equação admita solução não-nula:
E para usar a proposição 6.10, vamos escrever os vetores que aparecem em (i) em termos dos vetores LI .
Passo 3
A gente não tem o , né... maaaaasss a gente sabe que:
E podemos manipular isso:
Vamos pegar o e substituir já:
Passo 4
Voltando pra (i):
E substituindo tudo que a gente já definiu:
Substituindo agora o :
Vamos tirar esses parênteses (haja paciência, eu sei, mas vamos fazendo aos poucos):
E agrupando os vetores iguais:
E com isso ficamos com o sistema:
Passo 5
Pra resolver esse sistema a gente vai usar o Teorema de Cramer, que nada mais é que calcular o determinantes do coeficientes (tudo que está na frente dos alfa, beta e gamma) e igualar a zero. Tcharaaammm.. achamos o m.
Ufaa... acabamos... E aí? Conseguimos ajudar? Responde aí!