Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 6.2 - Ex. 28
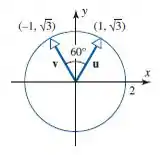
28. Os vetores e indicados na figura dada têm norma 2 e o ângulo de 60° entre eles em relação ao produto interno euclidiano. Encontre um produto interno euclidiano ponderado em relação ao qual e sejam vetores unitários ortogonais.
Passo 1
O produto euclidiano que ele fala no início do enunciado é o que fazemos quase sempre:
Maaaaas ele quer um produto interno euclidiano ponderado...
Passo 2
Para ser ortogona, o produto interno tem que ser zero:
E para ser initário, a norma tem que ser igual a um: (lembrando que a norma é o produto interno do vetor por ele mesmo)
Ps: não precisamos usar a norma dos dois vetores porque vai dar a mesma coisa.
Passo 3
Vamos substituir os valores e resolver o sisteminha que vai dar:
Então o produto interno euclidiano ponderado vai ser:
Resposta
Exercícios de Livros Relacionados
20. Seja { v 1 ,v 2 ,… , v r } uma base de um espaço com produto interno V . Mostre que o vetor nulo é o único vetor em V que é ortogonal a cada um dos vetores da base.
29. (Requer Cálculo) Sejam f ( x ) e g ( x ) funções contínuas em [ 0,1 ] . Prove:(a) ∫ 0 1 f x g xd x 2 ≤ ∫ 0 1 f 2 xd x ∫ 0 1 g 2 xd x (b) ∫ 0 1 f x + g x 2 d x 1 2 ≤ ∫ 0 1 f 2 xd x 1 2 + ∫ 0 1 g 2
27. Use métodos vetoriais para provar que sempre é retângulo qualquer triângulo inscrito num círculo de tal modo que um de seus lados seja um diâmetro. [Sugestão: expresse os vetores A B → e B C → da
23. Prove: se u e v forem matrizes n × 1 e A uma matriz n × n , então v T A T A u 2 ≤ u T A T A u v T A T A v